基于FPGA高阶FIR滤波器的实现

摘要：从FIR数字滤波器的基本结构模型出发，分析了FIR滤波器的设计思路及具体实现方法，详细介绍了FIR滤波器的分布式算法(DA)结构。通过分析计算，得到普通DA结构实现高阶滤波器会消耗大量的查找表资源，这样的资源消耗甚至令硬件资源不可接受。针对普通DA的不足，提出了改进型DA结构。并利用FPGA仿真软件分别时64阶FIR带通滤波器的两种改进型DA结构进行仿真，结果表明改进型DA结构所消耗的资源大幅度降低。从而验证了改进型DA结构在降低运算资源和提高性能等方面的优越性。

关键词：FIR数字滤波器；分布式算法结构；改进型分布式算法结构；FPGA

在航天航空系统、雷达系统、遥感遥测系统等领域都涉及到如何在较强的背景噪声和干扰信号下提取真正的信号，并随着系统对宽带、高速、实时信号处理要求越来越高，对滤波器的处理速度、带宽等性能要求也随之提高。数字滤波器的硬件实现方法主要有：DSP、专用芯片和FPGA。用DSP实现滤波器，其程序顺序执行，因此运算速度随滤波器阶数的增加迅速下降；专用芯片实现的滤波器功能相对单一，灵活性小；而FPGA具有灵活的可编程逻辑和并行处理等优点，可很好地实现信号处理的实时性，同时，开发程序的可移植性好，可以缩短开发周期，因此FPGA实现数字滤波器的设计越来越受到重视和广泛应用，本文数字滤波器的设计就是基于FPGA硬件实现。

1 FIR滤波器的基本模型

数字滤波器分为无限冲激响应滤波器(IIR)和有限冲激响应滤波器(FIR)，IIR滤波器与FIR滤波器相比，IIR滤波器容易取得较好的通带和阻带特性，FIR滤波器系统稳定且容易实现线性相位。系统稳定和线性相位对系统的设计至关重要，故对FIR滤波器的普通分布式(DA)算法结构进行了分析探讨与改进。FIR滤波器的网络传输公式可由式(1)表示：

式中：x(k)为输入函数；y(n)为输出函数；h(n-k)为滤波器系数；N为滤波器的阶数。根据式(1)，FIR滤波器的结构如图1所示。

2 FIR滤波器的设计及实现

2．1 FIR滤波器设计

FIR滤波器的设计方法有：窗函数法、频率抽样法和最佳一致逼近法。本文以窗函数法为例介绍一下滤波器设计。设窗函数为凯赛窗，通带截至频率fc、阻带起始频率fa、通带纹波δp和阻带纹波δa，则滤波器阶数N的计算如式(2)所示：

式中fs为抽样频率。由式(2)可见，通带和阻带的纹波系数越小，滤波器的阶数越高。因此在设计FIR滤波器时，需要在阶数，纹波系数和过渡带之间进行权衡，选出合适的模型。

2．2 FIR滤波器具体买现

相比用DSP实现FIR数字滤波器，采用FPGA实现可以获得更快的速度，同时还可采取各种算法降低运算资源，提高性能，分布式算法(DA)就是其中一种。随着大规模集成电路的发展，特别是可编程逻辑器件的发展，DA算法在数字滤波器硬件设计中的研究进一步加强。

2．2．1 DA算法结构

DA算法结构是将乘法运算转换成基于查找表的加法运算，其基本原理为通过比特串行运算产生两组内积结果代替乘法器结构，如式(3)所示：

式中：Ak为滤波器系数；xk为滤波器输入；N为滤波器阶数；y为滤波器输出。对于无符号数和有符号数xk的二进制表示式分别为式(4)和式(5)：

式中：xk，i为xk的每位二进制数，值为0或1；B为xk的二进制位数。将式(4)和式(5)分别带入式(3)中，可得式(6)和式(7)：

在滤波器设计中，一般采用有符号数，由式(6)和式(7)可知，有符号数的计算公式含有了无符号数的计算，因此本文以有符号数为例来介绍DA算法的具体实现。DA算法结构的实现过程如图2所示。

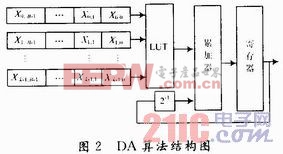
对于FIR滤波器来说，A0至AN-1为常数，因此由式(8)，式(9)和式(10)可看出，y的值仅与系数的各种组合有关，这种结构可以利用查找表来实现。设FIR滤波器阶数为N，系数的量化位数为M为，则需要存储器(ROM)深度和宽度的计算公式分别为式(11)和式(12)所示：