基于FPGA高阶FIR滤波器的实现

3．1 量化位数对滤波器影响

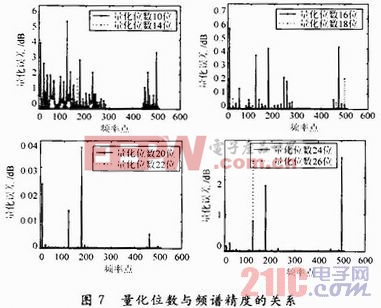
滤波器系数的量化位数与滤波器精度和消耗的硬件资源紧密联系，利用式(14)计算量化位数对滤波器精度的影响，量化误差如图7所示。

err(ω)=(f(ω)-f0(ω))2 (14)

式中：f(ω)为经过量化后的频谱特性；f0(ω)为标准的频谱特性。

由图7可看出，滤波器系数的量化位数越多，滤波器精度越高。当量化位数低于14位时会引入较大的误差；当量化位数高于16位时，通带内的量化误差约为0，阻带的量化误差的均值小于0．1能够满足设计的需求；当量化位数高于24位时，量化误差基本不变。综合频率精度，资源消耗和查找表的输出端口为4，设计滤波器系数的量化位数为16位。

3．2 滤波器具体实现

FIR滤波器的输入信号带宽为10 MHz，调制频率为70 MHz，调制系数为0．7的连续相位频率键控(cpfsk)信号，根据中频采样定理，采样频率为100 MHz，则输入信号的幅频和相频特性如图8所示。

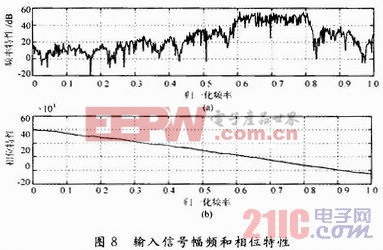
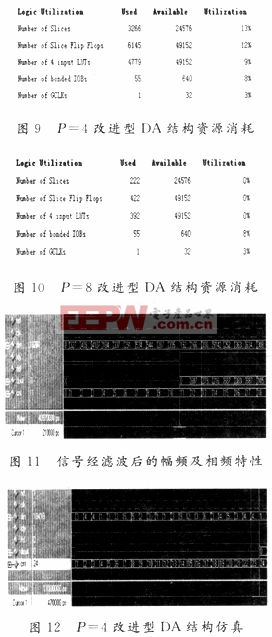
以Xilinx公司‘-10’的xc4vsx55芯片为FIR滤波器的硬件支持，应用Xilinx ISE 9．2i软件分析存储器个数P=4的改进型DA算法结构及存储器个数P=8的改进型DA算法结构设计的滤波器性能，其达到最高速度分别为237．206MHz和264．589 MHz，资源消耗分别如图9和图10所示。由图9和图10比较可看出，P=4的改进型DA算法结构所消耗的资源比P=8的改进型DA算法结构所消耗的资源高很多。图11和图12为两种改进型DA结构的仿真时序图，图中dout代表输出信号，cnt代表时延计算信号。从图11及图12可看出，P=8的改进型DA结构时延为24个时钟周期(470 ns)；P=4的改进型DA算法结构的时延为11个时钟周期(210 ns)。综上所述，与P=4的改进型DA算法结构相比，虽然P=8的改进型DA算法结构在时延方面存在不足，但其在资源消耗和速度等方面有明显优势。