基于载流导线循迹智能车的数学模型
—— 两个结论辅助数字模型运用
为了消除两个电路的差异,对(6)两边同乘以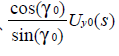 得:
得:
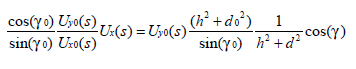
记
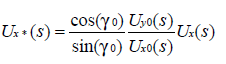
对(7)两边同乘以0()yUs得:
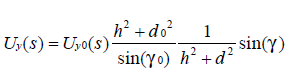
记向量![]() 。那么U
。那么U
的方向为![]() ,正是载流导线的水平垂直方向,我们用它来判断载流导线的走势;而由
,正是载流导线的水平垂直方向,我们用它来判断载流导线的走势;而由![]()
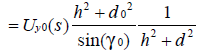 得
得
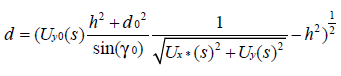
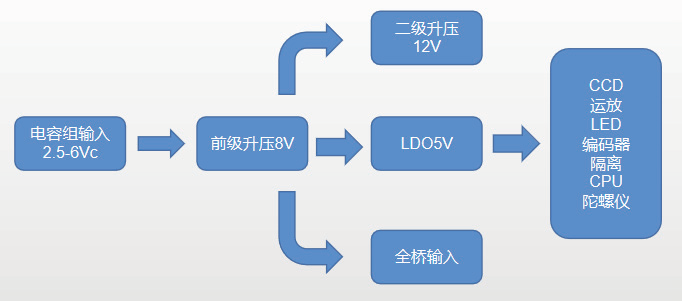
1.3 单竖直电感测距
如图4,电感竖直放置,离地高度h。易得
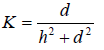
令![]() 运用法一得
运用法一得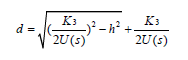 其中
其中
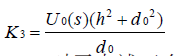
对于上述三个模型,我们可以测量一些有代表性的特征量。值得注意的是U0(s)好比一个基准时钟,是有相位的,但U0(s)和U(s)的相位必然相差0度或180度,具体原因笔者尚不清楚。若电路的输出电压无鉴相功能,如峰峰值、有效值、整流滤波输出值等只有正值,1.1的模型不需担心该问题,因为小车行进过程中U0(s)和U(s)始终同相,1.2则需通过其他算法判断导线在小车的左还是右,γ是正还是负,1.3也无法判断迹线在左还是右。
两个结论
以上推导是建立在无限长直导线的基础上的,但赛道是任意形状的,且电感会随着小车摆动,在这种情况下,上述几个数学模型是否还能适用呢?请看以下两个结论。
结论一:有限长直导线的K也是常数,故对于有限长直导线的循迹,仍可使用上述模型,当然精度会有所下降。对于任意形状的导线,导线可看作无数段有限长直导线的叠加[5],所以可以使用上述模型。
结论二:对于任意放置的电感,从导线电流到电路输出电压之间的传递函数,只有K不同,其他部分是一样的。所以小车行进过程中即使有摇摆,仍可使用上述模型。








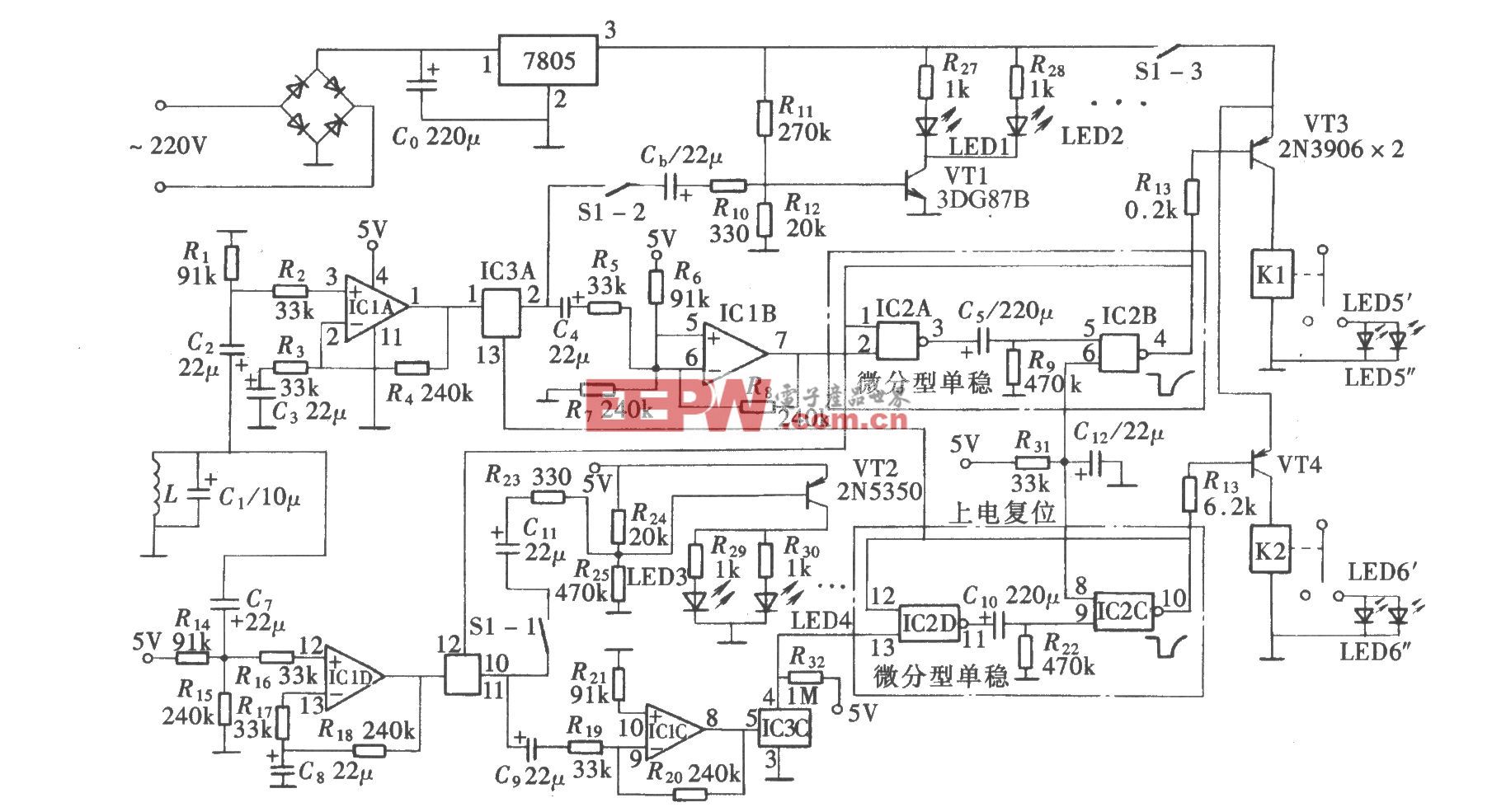

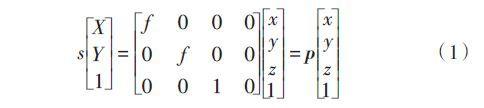




评论