基于载流导线循迹智能车的数学模型
—— 两个结论辅助数字模型运用
这种方法有几个优点:一是表达式与电路传递函数无关,即与电路无关,这就使得电路设计从理论上讲极其简单,只需满足线性时不变;二是表达式与赛道电流无关,这就使得该方法推导的模型从理论上讲具有极强的适应性;三是该方法推导的模型运用起来简单高效。
1.1 双一电感测距
如图1,两电感A和B水平放置,二者轴线与x轴平行,相距l,离地高度h。记![]() 下面将用到文献[4]的方法,以避免开根号。
下面将用到文献[4]的方法,以避免开根号。
A电感的变量用下标A表示,B电感的变量用下标B表示。
为了方便运用法一,不妨令
显然![]() , 易得
, 易得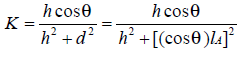 ,
,
那么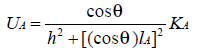 ,其中
,其中
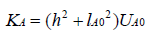
不妨假设θ较小,可以忽略。则
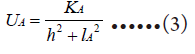
同理得 22BBBKUhl=+,其中
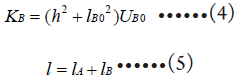
联立(3)、(4)、(5),解得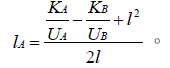 注意Al是有正负的。
注意Al是有正负的。
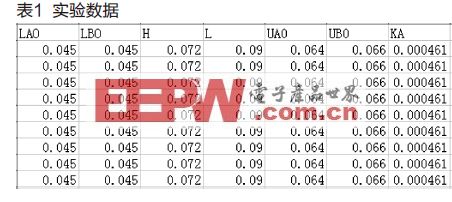
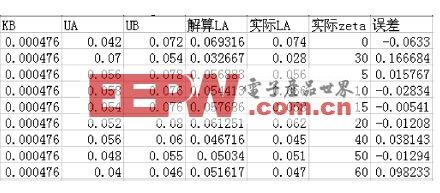
实验数据如表1。所有单位均为标准点位,电压是示波器读取的峰峰值,误差是未取绝对值的相对误差。
结论:除第二组外,其他组的误差都小于10%,大部分小于5%,且与赛道无明显关系。说明该数学模型正确,同时也佐证了法1.1的正确性。
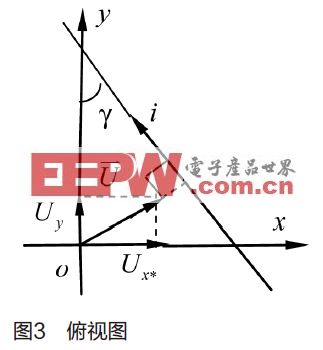
1.2 双水平正交电感测距、测方向
如图2所示,两电感xL和xL相互垂直。图3为俯视图,xL和yL置于原点o,xL和yL的轴向分别与x和y轴重合,o距地面高度为h,导线与y轴夹角为γ。xL和yL的相关变量分别以下标x和y表示。注意,xL和yL各自的电路传递函数是不相同的,下文会将其校正。
易得xL和yL的空间函数分别为

令00γ≠,运用法一可得
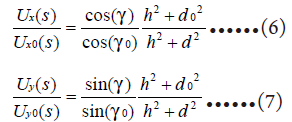













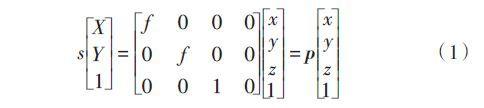
评论