基于FPGA的混沌加密虹膜识别系统设计(一)

　　)圆群,进一步把圆的半径r 作为变量，在a-b 平面得到由不同半径的圆CHi 构成的圆环。在a-b-r 空间中建立三维数组，数组中元素 ai,bi,ri P 的值代表a-b 平面上通

　　过点(ai，bi)，半径为ri 圆的个数。如果图像中存在满足方程(7-1)的圆，则

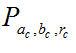
　　的值最大。即

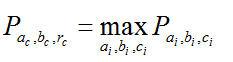
　　(7-2)

　　因此，数组中最大值元素所对应的参量(

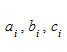
　　)就是图像中圆的中心和半径。

　　(2) Hough 变换的改进PHT 变换

　　上述变换方法虽然由使用广泛，但是因为它要在三维空间内搜索，计算复杂性较大，为此采用点Hough 变换，原理如图6所示，设K，L，M为圆周上三点，由圆的几何性质可知，KL 的中垂线L(KL) 与LM 的中垂线L(LM)必然相交于圆C 的中心O。设K、L、M 三点的坐标分别为

　　、

　　、

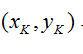
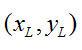
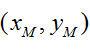
　　，则L(KL) 和L(LM) 的方程分别为：

　　L(KL):

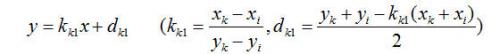
　　(7-3)

　　L(LM):

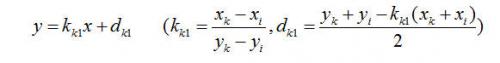
　　(7-4)

　　利用(7-3)和(7-4)式，计算出圆C 的圆心(

　　)和半径

　　：

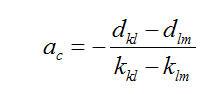
　　(7-5)

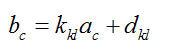
　　(7-6)

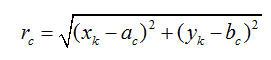
　　(7-7)

　　可见, 半径ri，中心(

　　)的圆周上任意不共线的三点(以下称为点组)对应a-b-r 空间中一点(

　　)，所以我们称之为点Hough 变换(Point Hough Transform)。

　　用向量

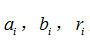
　　表示a-b-r 空间中的点, 则图像中圆(

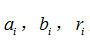
　　)上的点组对应于a-b-r 空间中的向量

　　。在图像中选取N 个点组，得到包括

　　，N 组来自同一圆上的点组对应的向量相同。向量组中不同编号的向量可能相同。向量组中出现次数最多的向量就是图像中圆的参量。用数组P[n](n=0, …, N-1)，表示向量组中向量

　　出现的次数，则有：

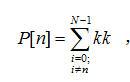
　　，其中 if(

　　)，kk=1 else kk=0 (7-8)

　　确定数组P[n]后,就可以找出图像中圆的参量值。

　　if

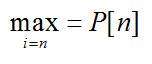
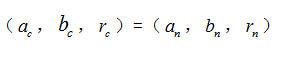
　　(7-9)

　　根据实际应用，我们将式(7-8)中kk=1的条件改为

　　，

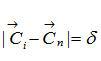
　　为一微小增量，更为符合实际应用。

　　PHT 不需搜索变量空间，只对选取的点组进行统计，计算复杂性决定于所选择点组的数目。

　　PHT 过程包括两个步骤：确定参量向量组和找向量组中出现频率最大的向量。设选取的点组数为M，从上述分析可知, 过程的计算复杂度为O(M)，过程最大数组是3×M。对于CHT 过程, 设图像中圆参量的取值范围分别为A、B、R，边缘点的数目为N。