基于卡尔曼滤波的电力系统短期负荷预测
2 卡尔曼滤波负荷预测模型
以连续若干天的同一时刻作为一组时间序列,来预测该时刻的下一个负荷值。通常,负荷值可以分为几个部分:
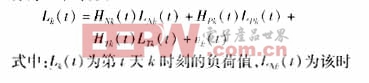
刻的基本负荷,Lpk(t)为前一天同时刻的的负荷值,LTk(t)为该时刻的气温,Vk(t)为误差,HNk(t)、HPk(t)、HTk(t)均为参数矩阵。由于预测的是某个时刻的值,所以式中的各个量都是一维的。
为方便应用卡尔曼滤波理论进行状态预测,特作如下变换:
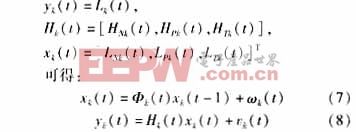
式中:yk(t)是观测值,Hk(t)为观测矩阵,Φk(t)为状态转移矩阵,Wk(t)为状态误差。由于在本文中状态变量是连续若干天的同一时刻的温度,它在短期的负荷预测中可以看成是缓变状态,因此可令Φk(t)=I,I为单位阵。

2.1改进模型
在实际预测过程中,一般可以提供预测时刻的气温预报值,或者通过几个点的预报值通过插值获得其他点的气温值。本文提出了预测值修正方法,即在此预测值的基础上加上温度修正值的负荷预测方法。
设待预测的第(t+1)天时刻负荷的卡尔曼滤波预测值为yk(t+1|t),该时刻的状态估计值为LTK(t+1|t),,而该预测时刻的气温预报值为Tk。状态估计值是卡尔曼滤波器通过历史负荷得到的对系统下一个时刻的状态的最佳估计,而预报获得的系统的新的状态值则反映了系统的未来状态,因此他们的组合能够让预测模型获得更多的信息,从而得到更加准确的预测值。为利用此信息,可以对预测得到的值进行修正,即在[Tk-LTK(t+1|t)]前乘以一个修正系数,即:
式中:bk为修正系数,可以通过试验获得,yk(t+1)为该时刻修正后的负荷预测值。
3 短期负荷的预测实例
用卡尔曼滤波以及改进后的模型对武汉地区电力负荷进行预测实例计算。在实践中初始状态xk(0|0),Pk(0|0)很难准确掌握。但由于卡尔曼滤波在递推过程中不断用新的信息对状态进行修正,所以当滤波时间充分长时,状态初值xk(0|0)对xk(t+1|t)的影响将衰减至近于零,初始协方差阵Pk(0|0)对滤波估计协方差阵Pk(t+1|t)的影响也将衰减至于零。因此,滤波的初始条件可以近似确定。
每一次递推运算中,要先求出预测值xk(t+1|t),然后根据预测值计算出预测误差的方差Pk(t+1|t),由最佳滤波规则计算卡尔曼增益Kk(t+1),经过卡尔曼增益的误差补偿后获得最佳滤波值xk(t+1),再由预测方程计算负荷预测值。
其中温度参数在待预测天以前由历史数据获得,并对其进行滤波估计,而待预测天的温度则由当天的温度预报获得。
引入误差指标:
相对误差:

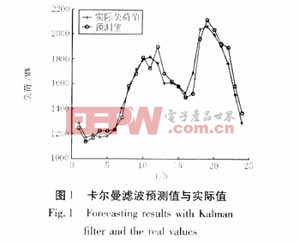
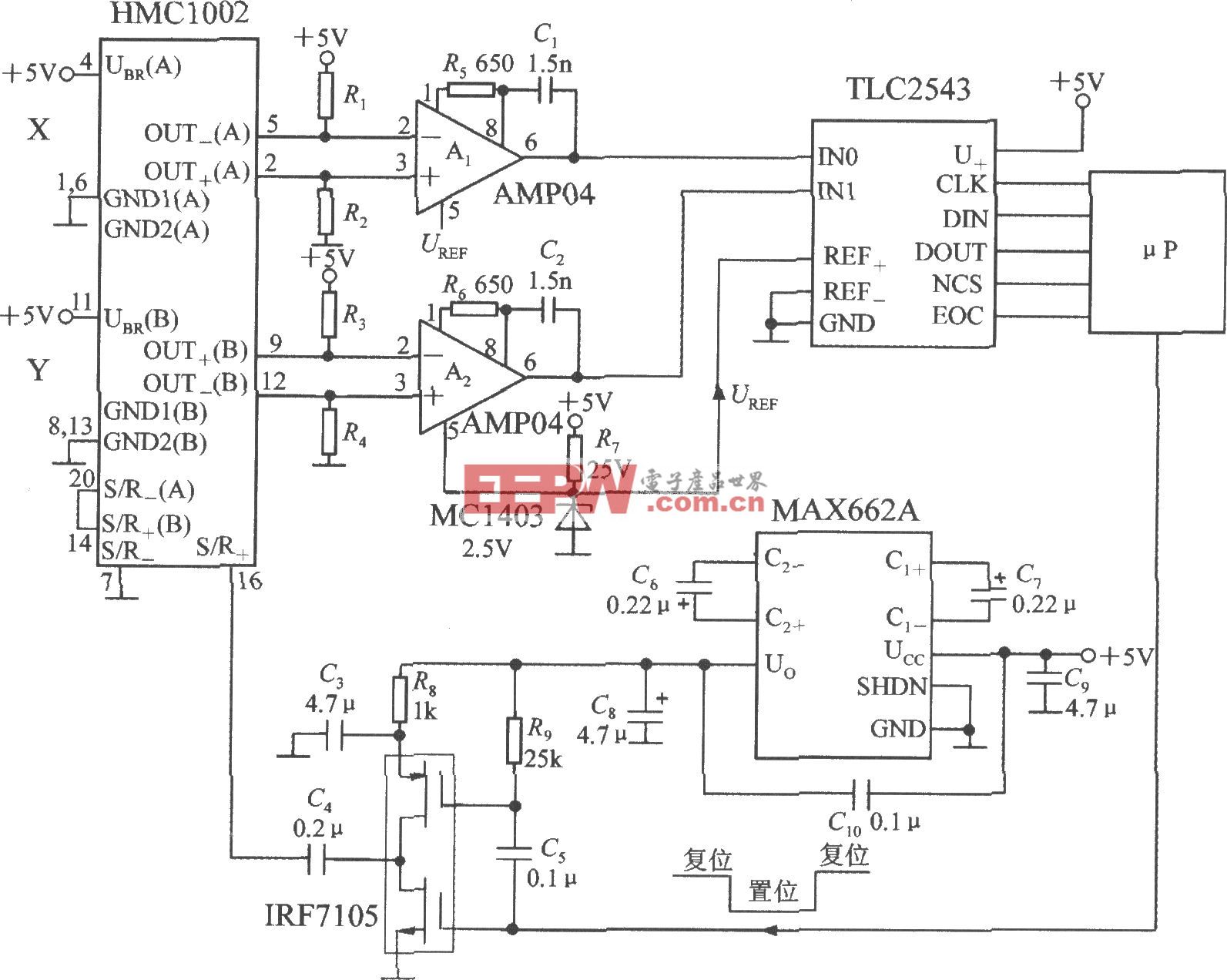
应用卡尔曼滤波模型以及改进后的模型对武汉地区的电力负荷进行实际预测,随意抽取某一天的预测结果及误差见下图(1)、(2)、(3)、(4)。本文引用地址:https://www.eepw.com.cn/article/179691.htm






评论