基于EKF的异步电机直接转矩控制系统仿真研究

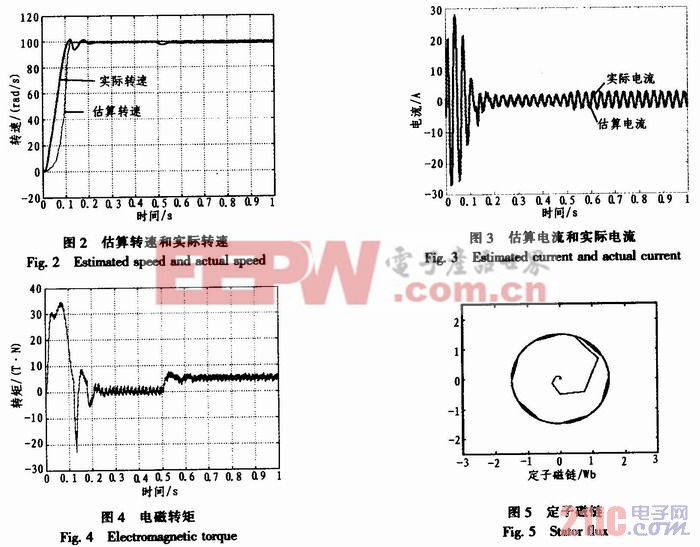
从仿真波形图2对比可以看出，采用无速度传感器控制算法后控制过程的上升时间比有速度传感器控制稍微长一些，但仍能满足系统性能指标要求。系统进入稳定后无速度传感器控制的效果和有传感器控制是一致的。图4显示的是突加负载后，从图3看出定子电流幅值稳定，转速变化很小并很快恢复稳定，输出转矩能很快达到给定负载转矩，体现了DTC控制系统转矩响应快的特点，由此可见电机在运行过程中，受到各种扰动时，电机转速稳定性好，可以满足对控制特性的要求。
EKF算法在异步电机转子速度估计的应用过程中采用直接更新系统状态量和协方差矩阵的方法，可以避免直接计算最大值动态范围较大的增益矩阵Kk。利用EKF算法的关键在于协方差矩阵Q和R的选取。Q与模登误差、系统分布、A／D量化误差有关；R与电流传感器噪声以及A／D变换器的编码误差有关。

4 结论
从算法分析和系统仿真分析讨论的结果，可以得出扩展卡尔曼算法在无速度传感器应用中的优点是：利用扩展卡尔曼滤波器可以不必了解电机的机械参数知识(可以克服电机参数反应灵敏的问题)，在电机启动过程中不必知道电机转子初始位置(可以解决电机的启动问题)，此外，EKF算法可以确保系统的全局稳定性(其他一些通过状态观测器实现电机无速度传感器控制的方法，通常仅在标称状态的轨迹上将电机非线性化，不能保证系统的全局稳定性)，而且整个系统易于数字化实现。但是扩展卡尔曼算法复杂，需要矩阵求逆运算，计算量大，为满足实时控制的要求，需要高速，高精度的数字信号处理器。另一方面，扩展卡尔曼滤波器要用到很多随机误差的统计参数，由于模型复杂，涉及因素多，使得分析这些参数的工作比较困难，需要通过大量调试才能确定合适的随机参数，而且调速范围有一定的局限性，只适合中高速调速系统。