分布式多视角目标跟踪算法在OMAP3平台上的实现与优化

　　3.3　跟踪精度优化

　　尽管3.1.到3.2.两小节提出的算法已经具有相对较高的鲁棒性，由于单个视角内的匹配误差会在视角间被传递甚至随着时间递推而被放大，因而提高视角内的跟踪精度也是关键。现实世界的视频的复杂性，使得视角内跟踪经常会遇到模板漂移的问题。针对上述问题，我们又实现了下面改进算法：抑制漂移的卡尔曼外观滤波(DIMKAF)[3-4]。DIMKAF(Drift-Inhibitive Masked Kalman Appearance Filter )算法通过计算模板像素真实值的概率分布定量地在线估计观测噪声的功率。状态转移噪声的功率也可以通过新息在线计算得到。这样，本算法的卡尔曼增益系数始终能够在更新模板与减少漂移之间寻求最优平衡点，十分有效地抑制了模板漂移现象，提高了有限搜索精度下的跟踪精确度。

　　4.算法在DSP上的实现难点与优化方案

　　视频跟踪算法具有运算量大的特点，这增加了算法在DSP上的实现难度。为了让算法能够实时地在DSP上运行，我们必须对算法中最耗时的部分进行优化。经过分析，算法中最耗时的部分为粒子滤波和模板匹配中的SSIM计算函数和插值函数。对于每一帧视频，算法要调用将近两百次的相似度计算函数和插值函数。粒子数越多，模板匹配的范围越大，则所需要的计算量越大。

　　优化过程分为算法优化和软件优化两个阶段。算法优化只在算法的层面上对计算公式进行优化，减少公式的运算量。软件优化主要是对程序代码进行优化，以提高程序的运行速度。

　　4.1　算法优化

　　本节针对粒子滤波和模板匹配中的SSIM计算函数进行了算法上的优化。

　　● 结构相似度指标第一步简化：分解简化

　　2.1节中介绍的粒子滤波和模板匹配中的SSIM指标[6]的计算方式，可以将其简化为如下形式：

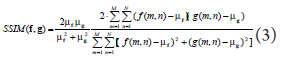
　　根据均值性质，上述式子可以化简为：

　　(3)式的运算量大约为10MN个加法和乘法运算，而(4)式的运算量仅为6MN个加法和乘法运算，运算量大约减少为原来的60%。

　　● 结构相似度指标第二步简化：模板均值方差复用

　　由跟踪算法可知， 在对同一帧视频数据进行处理时，模板是不变的，上式中的mf 以及ΣΣ==MmNnnmf112)),((是不变的，因此模板的均值和ΣΣ==MmNnnmf112)),((项只要计算一次，那么在其它SSIM的计算中可以重复利用，达到进一步降低计算量的目的。