高频雷达抑制冲击干扰的研究与实验
加入技术交流群
(4)
由X(τ,m)可换算出目标的速度.式(4)表示的是信号由多普勒域至多普勒谱域的变换.
若在基带信号重复周期k至周期l的时间段上，系统受到总长为(l-k+1)Tp的冲击干扰，且用n(t)表示干扰通过系统前端后得到的基带信号.n(t)的距离处理应为n′n(τ)=
.由于n(t)是系统带内白噪声，s(t)有理想低通频率响应，那么n′n(τ)是低通白噪声，其带宽等于s(t)的带宽W.在任一距离单元τ上，由于高频雷达扫频周期
，可以认为n′n(τ)和n′n+1(τ)是不相关的.因此序列{n′n(τ)}n∈［k,l］中的元素彼此不相关.
由以上分析可知目标的多普勒信号序列{xn(τ)}n∈［0,N-1］与冲击干扰的多普勒序列{n′n(τ)}n∈［k,l］存在明显区别：(1)目标的多普勒信号持续分布在整个时间段上，冲击干扰仅存在于有限时段上；(2)目标的多普勒信号与目标运动状态有关，有确定的变化规律，一般是连续可导的，而冲击干扰的多普勒信号是奇异信号.
三、多普勒域小波分析方法检测冲击干扰的方法
上面的分析表明冲击干扰在高频雷达多普勒域表现出区别于目标信号的奇异性特征，这一特征是检测和判断干扰时间位置的根据.Mallat在文献［2］中提供了使用小波变换检测奇异信号的方法，这种方法不仅可以确定奇异信号的位置，而且可以定量求得信号的Lipschitz指数.文献［2］指出负Lipschitz指数信号的小波变换结果表现为：小波系数模值随尺度减小而增大.而正Lipschitz指数的信号则相反.依据这一规律可以检测负Lipschitz指数信号的位置.在本文研究中，冲击干扰{n′n(τ)}n∈［k,l］的Lipschitz指数显然是负数，回波信号{xn(τ)}n∈［0,N-1］的Lipschitz指数是正数.如果区分信号Lipschitz指数的正负，则不必过多考虑小波函数的消失矩.因此这里选择小波函数主要考虑小波函数是否有好的时间-频率局部性质，以及是否具有正交性.
根据高频雷达多普勒信号是复信号以及杂波能量集中在低频部分的特点，本文提出利用小波分析技术在多普勒域检测冲击干扰的具体方法.这种方法使用多分辨分析的快速算法式(5)实现小波变换［3］.
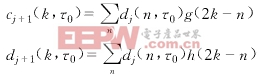(5)
式(5)中g(n)和h(n)分别是计算小波系数和尺度函数系数的滤波器，dj(n,τ0)表示尺度为2j时的尺度函数系数，cj(n,τ0)表示尺度为2j时的小波函数系数.图2给出相应的信号处理框图.多普勒信号的实部和虚部经过多分辨率分析，在不同尺度上得到各自的小波系数，构成新的复数序列.新序列的模与给定的门限进行比较，超过门限者被认为是存在冲击干扰的部分.
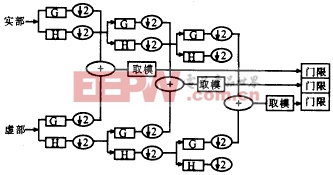
图2 小波分析检测冲击干扰算法框图 四、高频雷达抑制冲击干扰的原理 五、高频雷达抗冲击干扰实验 |
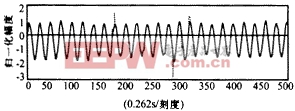
图3 高频雷达多普勒信号实部 实验中按图2的方法提取了多普勒信号的小波系数模值，图4(a)、(b)分别给出了尺度1、2的小波系数模值.实验中使用的滤波器h(n)={0.542，0.307，-0.035，-0.078，0.023，0.030，-0.012，-0.013，0.006，0.006，-0.003，-0.002}.g(n)={0.542，-0.307，-0.035，0.078，0.023，-0.030，-0.012，0.013，0.006，-0.006，-0.003，0.002} |
评论