TR-R2多站雷达系统的近程应用仿真与分析
本文引用地址:https://www.eepw.com.cn/article/153751.htm
vi为目标速度在Si——目标视线上的投影,νdi为Si中测得的目标多卜勒频移,
i=vi+v3.由式(16)解得vi,并以矢量
v=[q1 q2 q3]T (17)
表示目标速度,利用Si——目标视线的方向余弦(cosαi,cosβi,cosγi),将vi表示为
vi=q1cosαi+q2cosβi+q3cosγi,i=1,2,3 (18)
整理后写成矩阵形式解得
V=Φ-1μ (19)
式中
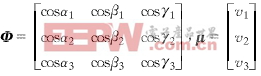
Φ为已知,因此可求得速度v,速度的数值由下式计算
(20)
五、速度测量性能分析
当各雷达站的频率测量相互独立,测量误差符合具有相同方差的零均值正态分布时,由于
1与νdi是线性关系,则
i也是正态分布的
(21)
式中σ2v为
1的方差,
0i为
i的均值,式(16)表明vi与
i是线性关系,故目标在各雷达站方向的速度投影vi也符合正态分布.同样式(19)表明qi与vi也是线性关系,因此qi也符合正态分布,其概率密度公式为
(22)
其中,
,为qi的均值,σ2qi=[k21i+k22i+1/4(k1i+k2i-k3i)2]σ2v为qi的方差,而kij=Δ′ij/Δ′,Δ′=det(Φ),Δ′ij为Δ的代数余子式.
根据式(22)写出q1,q2,q3的联合概率密度函数
(23)
式中B为qi的协方差矩阵,其元素为
B(i,j)=E[(qi-q0i)(qj-q0j)],μt=[q01 q02 q03]T
为求v的概率密度函数,对式(23)作如下的变量代换,令
q1=ξcosθcosφ,q2=ξcosθsinφ,q3=ξsinθ.
变换后的变量取值范围相应变为
此变换的Jacobian行列式为J=ξ2cosθ,这样ξ即v的概率密度函数可以写成

(24)
目标速度期望值及其方差分别为
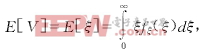
(25)
(26)
六、定位误差对速度测量的影响
目标速度估算是在定位之后完成的.由于速度估算公式中要用到Si——目标视线的方向余弦,这些方向余弦的精度取决于目标几何中心定位误差.因此,定位精度将直接影响速度测量精度.为便于分析,下面在考虑定位误差影响时,不考虑其它因素.
令δv为因定位误差所产生的速度误差,将速度v展为定位坐标的Taylor级数,在一阶近似条件下求得其偏移量计算式为
(27)
速度估计方差为

(28)
其中ε2i=2σ2
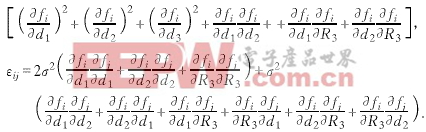






评论