TR-R2多站雷达系统的近程应用仿真与分析

假设目标坐标为(x,y,z)，发射机布在S3处.并设di为LTi与LT3之差，即

di=LTi-LT3=Ri-R3,i=1,2,3　(7)

根据距离关系，将站坐标Si(xi,yi,zi)和目标坐标代入式(7)展开整理并求解可得

rh=[x　y]T=W-1(β-d)

ra=[x　y　z]T=[f1(η)　f2(η)　f3(η)]T　(8)

式中　a=1+dTWTW-1d;

b=2rTh3W-1d-2dTW-TW-1β-2z3;

c=βTW-TW-1β-2rTh3W-1β-β3,

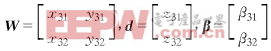
x3j=x3-xj,y3j=y3-yj,z3j=z3-zj,j=1,2

β3j=0.5(d2j+2djR3-ρ2j+ρ23),j=1,2

这里ρi与Si与原点的距离.

η=[d1　d2　R3]T=[η1　η2　η3]T.只要三个雷达站没有布局在同一直线上，W就是非奇异的，式(8)有确定的解.式中正负号的选取可参考文献[3]，但通过合理选择坐标系可以将目标置于上半球或下半球，从而使符号选取简化.

三、定位性能分析

1.定位坐标偏移量

当TR-R系统对目标定位时，直接测得量的d1,d2,R3，设测量误差矢量为

δη=[δd1　δd2　δR3]T=[δη1　δη2　δη3]T　(9)

目标定位误差矢量为

δra=ra-r0=[δx　δy　δz]T　(10)

其中r0为目标的真实位置矢量，由式(7)得

δηi=δLTi-δLT3=δLTi-2δR3　(11)

上式表明，δηi之间不独立.

设各雷达站对频率的测量相互独立，频率测量误差符合零均值正态分布.则各雷达站对距离的测量相互独立，且测量误差δLTi及δR3都符合零均值正态分布.而δηi与δLTi及δR3是线性关系，因而δηi也符号零均值正态分布，这时有

E[δηi]=E[δLTi]-2E[δR3]=0　(12)

但是，由于目标几何中心定位坐标与ηi的函数关系是非线性的，因此δηi将使定位坐标产生偏移.即使E[δra]≠0，偏移量的期望值可通过式(8)估算.

为求δra的数学期望，将ra=f(η)在r0附近展为η的Taylor级数，保留到二阶偏微分项，并考虑到δηi的相关性，可得定位坐标偏移量期望值的表达式

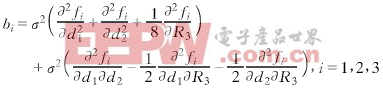
　(13)

式中σ2为单站雷达测距方差，b1，b2，b3分别表示坐标偏移量bx,by,bz.

2.目标定位误差的GDOP因子

一阶近似情况下，δra的协方差矩阵P为

p=E{(δra-E[δra][δra-E[δra]]T)}=FSFT-bbbTb　(14)

其中　　bb=[bx　by　bz]T，

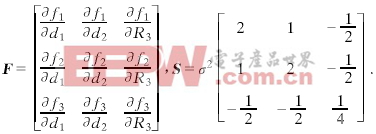
P的对角线元素为定位坐标方差σ2x,σ2y,σ2z.目标定位误差的GDOP因子为

　(15)

四、目标速度测量

在0-Ti时段系统发射单频脉冲，已经测得运动目标回波的多卜勒频移，由此可求得目标速度在相应方向的投影，将这些投影看做空间矢量，就可估计目标速度.

在TR-R2多站雷达系统中，S3构成单站雷达的同时还分别与S1，S2构成双基地系统.根据单站与双基地系统多卜勒关系得到方程

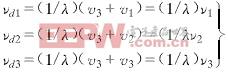
　(16)