基于中档FPGA多相滤波器的设计实现

　　除了任何寄存器和一般用途的逻辑，常规8抽头FIR滤波器中的每个抽头包含一个乘法器和一个加法器，当然为我们提供了总共8个乘法器和8个加法器。滤波器之后需要一些额外的逻辑，以便丢弃任何不想要的样本。

　　同样，在我们最初的4 × 2抽头多相实现中的每一个抽头含有一个乘法器和一个加法器，再次为我们提供了总共8个乘法器和8个加法器。在多相实现中，需要实现“旋转开关”送入滤波器的逻辑数量大约相当于在常规8抽头FIR滤波器中丢弃不要的样本所需的逻辑。

　　当然，多相实现还需要一些额外的逻辑和一个加法器累加来自四个子滤波器的结果。因此，最终的结果是，最初的多相实现需要比传统的8抽头FIR滤波器更多一点的逻辑。

　　然而，对于传统的8位FIR滤波器，在每个时钟都要执行8次乘和8次加。相比最初的多相实现的情况，在任何主时钟时刻，只有一个子滤波器是工作的。由于在这个例子中每个子滤波器含有两个抽头，这意味着这个功能的滤波器部分在每个时钟只进行两次乘法和两次加法。

　　当然，从四个子滤波器收集结果的求和功能还必须在每个主时钟进行加(在每4时钟周期开始时，这个累加器清零;它从四个子滤波器收集结果; 在每4时钟周期结束时，它产生一个新的值)。

　　这意味着，最初的多相实现的每个子滤波器有效地以常规8抽头FIR滤波器1/ 4的频率运行。反过来，这意味着最初多相实现只在每个主时钟进行两次乘法和三次加法(包括加法器的加操作)，从而大大节省了功耗。

　　此外，在最初的多相实现中，由于四个子滤波器的每个只用了1/4的时间，这意味着在任何特定时间，我们实际上只需要其中的一个，这使我们更加完善了实现方法，如图14所示。

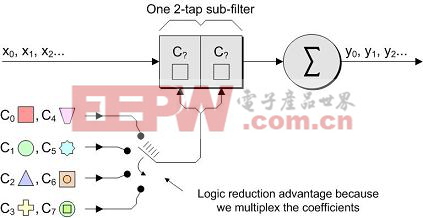
　　图14 更完善的基于多相滤波器的抽取器实现方案

　　在这种情况下，我们采用了单一的2抽头子滤波器，每个抽头含有乘法器和加法器。在每个主时钟，我们选择合适的系数对。每一个抽头需要额外的寄存器和用于维护的逻辑，但与减少的乘法器和加法器相比，与我们的最初多相实现相比，这是微不足道的。

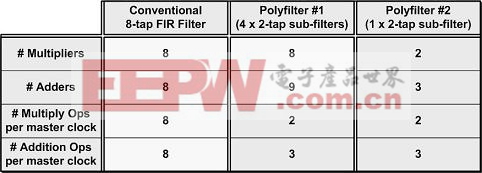
　　当然，在我们原来的多相实现中，我们仍然要在每个主时钟时刻执行两次乘法和三次加法，。这些抽取实现例子的总结如表1所示。

　　表1抽取实现实例的总结

　　利用多相FIR滤波器进行内插

　　现在让我们来考虑内插的情况。首先让我们先考虑一个基于常规8抽头FIR滤波器的内插子系统的符号表示，如图15所示。

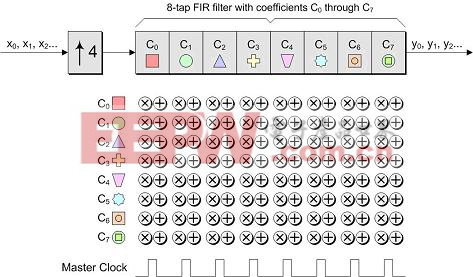
　　图15传统的基于8抽头FIR滤波器的内插器的符号表示