六西格玛水准的产品设计,我们做得到!
接触过六西格玛管理的朋友都知道:所谓的“六西格玛的质量水平”,是指每百万个产品中只有3.4个缺陷产品,甚至更少。这相当于产品的Cp>=2,Cpk>=1.5的结果。要达到这样近乎完美的质量水平,仅仅依靠生产阶段的管控是不够的,往往需要在设计阶段就要做好公差设计(也称“容差设计”)。
本文引用地址:https://www.eepw.com.cn/article/249155.htm公差设计ToleranceDesign是研发三阶段(系统设计、参数设计和公差设计)中的最后一环,它是指在参数设计阶段确定的最佳条件的基础上,寻找各个参数最佳的容许误差,使得质量和成本综合起来达到最佳的经济效益。相对于系统设计和参数设计而言,公差设计是最容易被忽略的一环。这一方面是因为人们对质量波动的理解不够深入,更重要的是缺乏一个成熟的公差设计的工具软件,使得企业在推行六西格玛设计时很难落地。
笔者根据近几年的研发项目实践,在很多企业已配备的统计质量管理软件JMP平台上总结出一个切实可行的公差设计解决方法,供有六西格玛设计需求的技术人员参考。
下面,结合一个在汽车、机械、电子等行业适用面都比较广的基础机械系统设计案例,介绍一下公差设计的原理及其计算机实现方式。
在一个装配环中装入3个零件,如下图所示,技术要求间隙(Gap)的目标值T=0.015,LSL
=0.005,USL=0.025,也就是Gap的长度要求满足0.0150.010。加工的零件1、2、3的平均值p=1.554,标准差p=0.001,而装配环的平均值e=4.674,标准差e=0.002。假设所有部件的参数均已实现六西格玛的目标,
试问:该系统公差设计的能力如何?如果未能达到六西格玛水平,应当如何改进?

容易看出,间隙与装配环及3个零件的设计关系是:
=0.012
所以,当前的缺陷数,由此转化得到的西格玛水平只有4.15(考虑1.5个sigma偏移,下同),没有达到六西格玛的目标。
如何改进呢?常见的有两种方法:调整均值或降低标准差。
1.第一次改进
调整均值是相对简单的一种方法,运用JMP软件中的预测刻画器(其后台运用的是数学中的优化论OptimizationTheory),实现起来就更方便了。从下图可见,当装配环的平均值调整到4.677,零件的平均值保持1.554不变,就能使间隙均值增大到0.015,与目标值重合。这时候的缺陷数PPM降到了157,由此转化得到的西格玛水平也提高到5.10,但仍未达到六西格玛的目标。
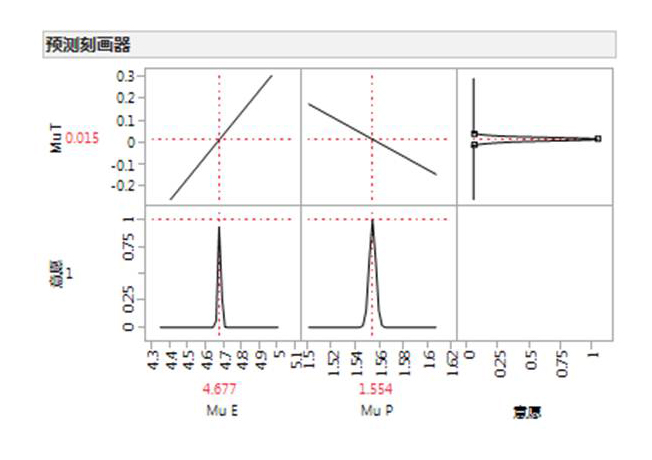
2.第二次改进
在调整均值的功效发挥到极限之后,还可以使用降低标准差的方法来进一步优化设计。那么应该让装配环和3个零件的标准差降到多少呢?从本质上讲,答案是下述这个方程式的数值解:
这本来是一个很复杂的数学问题,涉及到计算机编程技术。但基于上述公式利用JMP软件中的预测刻画器及其内置的意愿函数功能,方程式的求解变得方便了很多。如下图所示,当装配环的标准差降低到0.0016171,零件的标准差降低到0.0008205时,缺陷数PPM就等于3.4了,也就是我们梦寐以求的六西格玛水平。
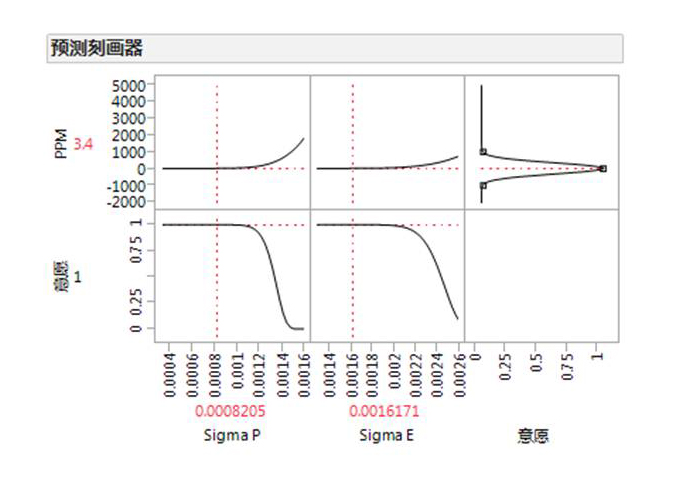
3.第三次改进
有些人可能对第二次改进的结果已经很满意了,但还有些人却还会感到有些不足:能否根据实际需要事先指定标准差改进的比例?具体地说,在系统从5.1个西格玛向6个西格玛优化的过程中,能否分配其中30%的改进来自于零件,70%的改进来自于装配环呢?这个业务需求其实可以转化成以下三个方程式:
求解这个方程组是一个更加复杂的数学问题,需要的编程时间也更长。所幸的是,同样基于这个方程组,利用JMP软件中的预测刻画器及其内置的意愿函数功能,方程组的求解难题被轻松解决。如下图所示,当装配环的标准差降低到0.0015311,零件的标准差降低到0.0008738时,缺陷数PPM也会等于3.4,而且装配环标准差的改进比重恰巧等于事先指定的0.7,零件标准差的改进比重恰巧等于事先指定的0.3。
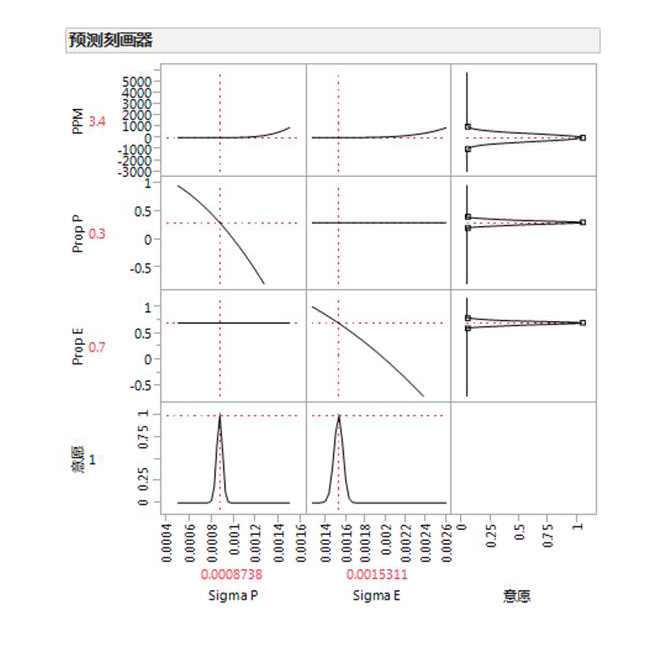
显然,这种改进方式有利于工程师们更积极地参与公差设计的过程,将较多的改进比重分配给容易优化、成本低廉的部件,较少的改进比重分配给不易优化、成本昂贵的部件。
总之,通过巧妙地使用一些现成的统计分析工具,我们发现:公差设计并不遥远,达到六西格玛水准的产品设计也是可望又可及的,由此而设计并制造出来的产品质量必然会更加稳健和可靠。









评论