基于数字随动系统的PWM装置数学模型分析
摘要:通过分析SKJ-II型数字随动系统中PWM装置的工作原理,建立了模型公式并推算出理论传递函数关系。根据模型公式得到了PWM装置系统化的理论传递函数,并通过实验验证了理论传递函数的正确性,并指出模型中电源电压需要考虑开关的管压降问题。对于应用PWM技术进行功率变换的控制系统的建模有理论指导意义。
本文引用地址:https://www.eepw.com.cn/article/160580.htm1 引言
目前,直流PWM调速系统凭借开关频率高,低速运行稳定,动态性能优良等优点,应用日益广泛,特别是在中、小容量的高动态性能系统中。
PWM控制与变换器(简称PWM装置)是直流脉宽调速系统中的重要组成环节,而对于PWM装置的数学模型,文献中仅给出最后近似的传递函数,并未解释其中框图变换的过程和参数分析。SKJ-II型数字随动系统内部含有调速环,其中就包含PWM装置,这里基于该系统中使用的PWM装置模型进行拓展分析,以便获得其模型的推导及变换过程,为PWM装置模型提供必要的理论依据。
2 模型建立与框图分析
SKJ-II型数字随动系统的结构如图1所示。功率放大器环节起到PWM控制器和PWM变换器的作用。
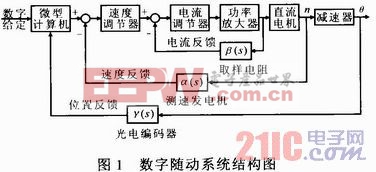
为了方便研究,将功率放大器环节内容分为两步,分别简称为PWM控制器和H桥,UX11(s)信号作为PWM装置的输入,Ud(s)为PWM装置的输出,ρ(s)为中间量。
2.1 静态分析
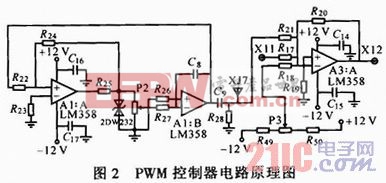
实现PWM控制器的电路如图2所示。预建立PWM装置的模型,先确定其输入信号,输入信号为UX11(X11端输入信号),该信号由系统前端的电流调节器的输出决定。图中,XJ7端为三角波发生电路的输出端,三角波发生电路中运算放大器A1:A构成加法器,运算放大器A1:B构成反向积分器,电位器P2主要用来控制产生的三角波的频率,2DW232是双向稳压二极管,起了限幅的作用。运算放大器A3:A以及外围电阻构成了一个反相加法放大电路,由于放大倍数较大,故小信号时才线性放大,大信号时会工作在非线性饱和状态。
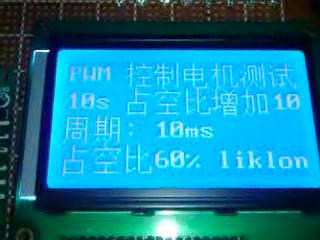
当X11端输入信号接地,即UX11=0 V时,利用GDS1102A数字示波器测量XJ7端和X12端的波形,分别记为uXJ7和uX12,两者波形如图3所示。
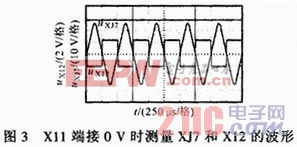
当uXJ7较小时,反相放大倍数为50;当uXJ7较大时,运算放大器A3:A会饱和,输出波形是正负对称的梯形波,但图中输出波形很接近矩形波,称该梯形波为近似矩形波,其占空比是50.81%。
PWM控制是对脉冲的宽度进行调制的技术,在此通过调制近似矩形波的占空比来实现PWM控制。当X11端输入电压信号,则近似矩形波占空比会产生相应改变。当运算放大器A3:A工作在线性状态,忽略调零通路作用,则流过R18电流为零,规定电流经R21,R20,R17一端流向R21,R20,R17的公共端为电流的正方向,并假设运放为理想运算放大器,根据KCL定理可得:
iR21+IR17+iR20=0 (1)
根据理想运算放大器的性质可知UA3_2=0 V,由欧姆定律可得:

分析X11端输入UX11为零时情况,记X12端饱和输出电压为+U0。当uX12=-U0(即负饱和)时,代入式(3)可得:uXJ7=U0R21/R20;当uX12= U0(即正饱和)时,代入式(3)可得:uXJ7=-U0R21/R20。记XJ7端输出三角波的幅值范围为[-U1,U1],周期为T,则有X12端输出梯形波单个周期的线性放大时间t1、输出正饱和时间t2、输出负饱和时间t3为:
t1=(R21U0)T/(R20U1),t2=t3=0.5(T-t1) (4)
按照矩形波占空比的定义,则有PWM控制器输出矩形波的占空比为:
![]()
当然,实际输出波形并非理想的矩形波,而是梯形波,具体梯形波如何描述占空比暂且不讨论,假设各周期内线性区工作时间t1相对于这个周期的总时间T非常小,则可忽略其线性区时间t1,则X12端输出矩形波的占空比ρ=t2/(t2+t3)=0.5。
由上述推算可以得到结论:当输入UX11=0 V时,若uXJ7为正负对称的理想三角波,则运放器A3:A的反相端输入信号(R20/R21)uXJ7依然为正负对称的三角波。X12端占空比为50%,即输出负饱和时间与输出正饱和时间相等,实验测试结果如图3所示,示波器中显示占空比为50.81%,有1.62%的误差,除了示波器的测量误差还应注意此处计算占空比忽略了线性区时间t1。
pwm相关文章:pwm原理








评论