基于FPGA的FFT算法优化及其在磁共振谱仪中的应用
加入技术交流群
2 FFT算法实现
FFT算法在FPGA上实现的过程中，信号的值、系统的系数和运算中的结果都存储在有限字长的存储单元中，从而导致了设计时的无限精度转变成实现时的有限精度，必将产生相对于原设计系统的误差，严重时会将由于双通道不平衡产生的镜像峰湮灭，从而使整个设计失去意义。
为了实现FFT实时运算，基于FPGA的FFT信号处理模块是关键，并且要求此模块能在频率至少为210 MHz的系统时钟下稳定工作。同时又因为并行的FFT设计需要占用大量的资源，资源使用率过大会制约布局布线后的时序收敛。为了平衡资源与速度间的矛盾，整个设计通过64点FFT并行模块的复用来实现。
2．1 有限字长效应及其优化措施
在FFT算法中，采用蝶形计算，如图3所示。
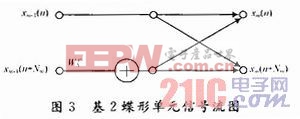
对于基2时间抽选FFT算法，蝶形公式如下：
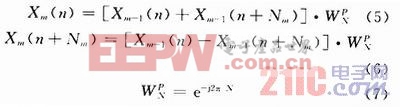
式中：N为FFT点数；Nm和P为两个同迭代次数m有关的量；Xm-1为ADC输出信号经过m-2级蝶形运算得到的计算结果；旋转因子
由式(7)给出，每个蝶形包含两个复数乘法。
由于存储单元有限，必须对计算结果截取，进行定点化，但是同时又会引入舍入误差en，这种现象即为有限字长效应。考虑到每个复数乘法相当于4个实数乘法，因此有限字长时复数乘法的实际乘积可以表示为：
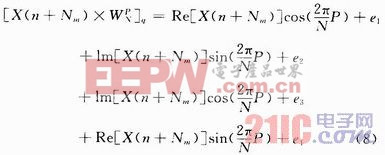
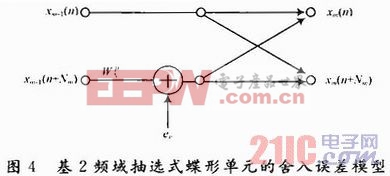
式中e1，e2，e3，e4分别为其对应的实数乘法的舍入误差。因此可进一步建立如图4所示的蝶形计算舍入误差模型。
评论