OFDM系统中频域同步技术及FPGA实现

整数倍频率偏移估计模块

将相关单元输出的复数据的实虚部符号位送到整数倍频偏估计单元中进行整数倍频偏估计。为了节省芯片资源，这里我们将估计整数倍频偏的算法加以简化，用相关后的复数据在导频位置上的实虚部的符号位来估计整数倍频偏值。下面的仿真的电路波形图证明这样实现整偏估计算法是可行的。它的输入为相关单元输出的复数据实虚部的符号位和此复数据的载波同步位置，输出为整数倍频偏估计值。

小数倍频率偏移和采样钟频率偏移模块

首先对相关单元模块输出的复数据的实虚部进行归一化，然后求归一化单元输出的16位复数据的相角，同时用RAM的读地址和读使能信号分别控制读取存有矢量A和矢量B数据的ROM表中的数据。其中矢量A和B分别为线性最小平方估计算法中矩阵AT的第一行和第二行矢量，用此相角分别和读出的矢量A和矢量B在一个符号内进行相乘累加，再根据保护间隔的不同，乘以相应的系数，便可分别得到小数倍频偏和采样钟频率偏移的估计值。

细定时估计模块

考虑到定时估计范围的问题，该模块利用四个符号的散布导频进行定时估计。将当前符号的散布导频值及从RAM中读出的前三个符号的散布导频值按一定顺序排列，并做相邻导频相关。将相关后的复数据的实虚部分别取绝对值累加，并将二者的累加和进行归一化处理后进行查表，从而得出复数的相位值。这个相位即为符号定时偏移所引起的旋转相位。再对此相位做如公式(6)的运算，这样就得到了符号定时偏移的整数和小数部分的和，然后将其送到求整函数中，从而得到符号定时偏移的整数部分。将这个值经过并/串变换后送到前端时域同步部分，去调整FFT窗位。

电路仿真

其仿真条件为：瑞利信道，SNR为15dB，载波频偏设为-14.9倍子载波间隔(即整数倍频偏值为-15，小数倍频偏值为0.1倍子载波间隔)，采样钟偏移为50ppm，保护间隔长为512，定时符号偏移为-100个采样点。此电路工作频率为10MHz。输入的16位复数据由MATLAB仿真程序产生的。

整数倍频率偏移电路仿真

由于电路波形中无法表示小数，因此将各小数进行“扩展”，其表示皆为二进制数据，以下同。在图4.1中，out_re[31]和out_im[31]分别是前后两个OFDM符号中对应子载波相关结果的实虚部的符号位，int_freqoffset[5..0]和syn_int分别是整数倍频偏估值和其有效起始位置脉冲。

图4.1 整数倍频偏估计部分的电路仿真波形图

由于整数倍频偏在每一符号的结束处才能估计出来，所以syn_int在每一个符号的结束处出现，其后即为当前符号的整数倍频偏值。由于本算法利用了4个符号的连续导频，故图4.1中，从第四个syn_int后的int_freqoffset[5..0]才是当前符号的整数倍频偏估计值。由仿真波形可看出，估出的整数倍频偏与仿真数据中所假设的一致。故用此算法的简化形式可以准确地估计出整数倍频偏值。

小数倍频率偏移及采样钟频率偏移估计的电路仿真

sernum[1..0]表示前级输入的符号类型;syn为输入复数据中的有用数据起始脉冲;rein[15..0]和imin[15..0]分别为FIFO模块输出复数据的实虚部;syn_offset为小数倍频偏和采样钟偏移估计结果的起始位置;fri[14..0]和qdelt[14..0]为小数倍频偏估计值和采样钟偏移估计值，它们由1位符号位和14位小数位组成。这里的小数位数是根据其估计范围和估计精度要求来确定的。

在图4.2中，小数倍频率偏移和采样钟频率偏移估计模块使用连续导频进行估计。在每个符号末，syn_offset高电平有效时，fri[14..0]和qdelt[14..0]才是当前符号的小数倍频率偏移和采样钟频率偏移估计值。波形中的估值与实际数据的对应关系如表4.1所示。

图4.2 小数倍频偏和采样钟偏移估计单元的电路仿真波形图

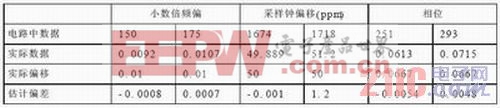
表4.1 波形图中数据与实际数据对照表

小数倍频率偏移和采样钟频率偏移模块是在整偏校完之后才有效，此时的小数倍频率偏移是经过时域粗偏估计校正后的剩余部分。表4.1列出波形中的估值与实际数据的对应关系。从表中的数字对应关系可以看出，电路中估计的小数倍频偏与实际频偏的差在0.1%以内。采样钟偏移估计值与实际偏移误差为1ppm左右，这已满足了采样钟的粗调精度;相位输出为前后符号的小数倍偏频所引起的相位旋转。由此单元电路，可以准确地估计出小数倍频偏和采样钟偏移及其相位。