基于FPGA的数字三相锁相环优化设计
3 三相锁相环的FPGA设计
3.1 未优化的三相锁相环的FPGA结构
根据图1三相锁相环的拓扑结构及原理,三相锁相环的基本硬件结构如图3所示。
首先通过采样,将三相电压离散化并处理为32 b有符号数,经过Clarke变换与相应的参数相乘后相加得到两相静止坐标的分量μα,μβ。共有5个乘法运算,3个加法运算。然后是Park变换,在此三相锁相环中只需要μq分量,需要2个乘法运算,2个三角函数计算,1个加法运算。后面的PI控制器需要2个乘法运算,2个加法运算。最后是VCO需要2个加法运算。整个运算过程共需要9个乘法运算,9个加法运算,2个三角函数运算。
从对三相锁相环的基本结构分析可知,整个过程需要9个乘法运算,2个三角函数运算。在FPGA中实现乘法运算和三角函数运算会消耗大量的资源。特别是传统的查表法三角函数运算在消耗大量资源的同时还存在精度问题。
3.2 三相锁相环的优化设计
由于该设计采用25 MHz的系统时钟,而采样频率为5 MHz,所以设计的时序余量非常大。依据面积和速度的平衡与互换的基本原则,针对乘法运算多的特点,采用乘法复用,系统中只保留一个乘法模块,通过合理选择,达到时分复用。
在Park变换中存在的三角函数运算,可以通过CORDIC算法优化。CORDIC算法是通过基本的加法和移位运算来代替乘法和三角函数运算的,特别适合矢量旋转的运算。使用迭代的方法,多步完成要旋转的角度。CORDIC算法可以实现如式(6)所示的运算。
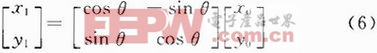
式中:x0,x1为初始坐标;θ为要旋转角度;y0,y1为最终的坐标。通过对式(6)的分析与Park变换相比较可以发现,只要把角度取负,就可以通过CORDIC算法完成整个Park变换的运算。
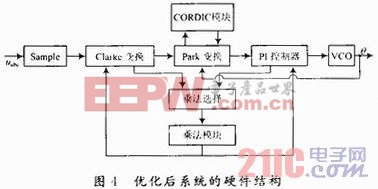
优化后系统的硬件结构如图4所示。本文引用地址:https://www.eepw.com.cn/article/189839.htm
4 结语
本文分析了三相锁相环的基本原理。针对FPGA的特点对锁相环进行了优化设计,并利用Verilog HDL硬件描述语言编码实现。该设计可直接用于PWM整流器、UPS等控制系统中。
fpga相关文章:fpga是什么
锁相环相关文章:锁相环原理









评论