脉冲变压器的磁学

NI=H×磁路长度，则

NI=Hairlg＋Hcorel=Hcore(μrlg＋l)

对上式重新排列，可写出磁心的磁场强度：

Hcore=NI/l(1＋aμr);（18）

式中a=lg/l(0≤a≤1)

　　式（18）表示有空气隙磁心内部的磁场强度为没有空气隙磁心内部磁场强度的1/（1＋aμr）（假设lg和l相比是很小的）。按照这一关系，如要求有空气隙磁心的磁场强度进入饱和区，则要求加在磁心上的安匝数增加(1＋aμr)倍。

　　实例：一个具有等效磁路长度为5cm、相对磁导率为5000、总的空气隙长度为0.1mm的铁氧体磁心在数值NI左右进入饱和区。它比等效没有空气隙的磁心所要求的安匝数要高出11倍。

　　在通信系统中，当有直流电流流过变压器的绕组时，为了防止磁心饱和，使用有空气隙磁心是常见的。使用大的空气隙磁心会导致边缘效应加大（因为不是所有磁通都包含在气隙内部），它也会使匝间漏电感和杂散电容增大。

　　磁性材料的饱和点μ=0，考虑到e=－NdΦ/dt=－NAμdH/dt，所以如μ=0，则e=0。即变压器丧失变换的功能。

　　如同H∝i一样，一般电感器的电感量∝μ，因此，当μ=0时，电感等于零。

　　超出磁心的饱和点以后，则变压器丧失它的功能。

3变压器等效电路

　　研究理想变压器的假设条件是：

　　（1）磁心材料有足够大的磁导率，其值可等效地看作是无限大(μ∞)；

　　（2）励磁电流足够小，其值可等效地看作是零（im=0）；

　　（3）磁心的任何损耗都小到可以忽略；

　　（4）线圈绕组的电阻小到可以忽略；

　　（5）所有绕组之间的磁通都是完全耦合，没有磁通“泄漏”（k=1）；

　　（6）绕组间的电容小到可以忽略。

　　但实际变压器不是这样的。下面我们将研究实际变压器的等效电路。

3.1有限磁导率

　　如果μ是有限的，则im将不等于零，在原边绕组中就有励磁电流存在。

　　从式（9）和（10），可写出：

i1=ΦRm/N1＋N2i2/N1=im＋ni2

式中im是励磁电流。这一增加的电流可以在等效电路中增加一个和原边线圈并联的电感Lm来表示，如图10所示。

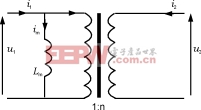
图10磁心励磁电流

3.2磁心损耗

　　（1）磁滞损耗

　　在2.6节已叙述了环形磁心B－H之间的滞后关系以及和磁滞回线闭合曲线面积成正比的损耗。闭合曲线面积和频率成正比，在频率是恒定时（尽管对脉冲变压器来说，变压器工作频率的变化率是一含糊的概念），从实验推导出的磁滞损耗公式是：

Ph=khBmax1.6(W)(19)

式中kh—是材料的磁滞损耗系数。

　　（2）涡流损耗

　　由法拉弟定律可知，当磁心中磁通交变时，磁心中亦会产生感应电动势，这个感应电动势会在磁心材料上产生环形电流，这个电流会在磁心的有限电阻上引起功率损耗。这个损耗和频率的平方成正比，但在频率基本恒定和磁通近似均匀分布时可得：

Pe=keB2max（W）(20)

式中ke—是材料的涡流损耗系数。

　　（3）磁心损耗

　　磁滞损耗和涡流损耗两项合并，就能求得磁心损耗近似值的有用模型。

Pc=khBmax1.6＋keBmax2≈αΦ2max

式中Φmax和电压U1max成正比，所以Pc∝U1max2。虽然这仅仅是一个不严密的近似，但它使我们能用一个并联在原边绕组两端的等效电阻RC来作为磁心损耗的模型，如图11所示。

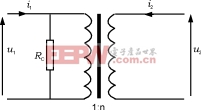
图11铁心损耗的等效电阻

　　为了减小磁心损耗，可用高电阻率的磁性材料（如铁氧体磁性材料）或用能减少涡流电流的磁心结构（如叠片铁心）。

3.3绕组电阻

　　用来绕制变压器线圈的导线，其电阻不为零，所以它将在每一绕组上产生电阻损耗。为此在等效电路中每一线圈上增加一个串联电阻，如图12所示。

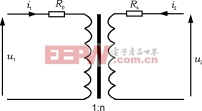
图12绕组电阻

　　为了减小绕组损耗，应尽量用较大截面积的导线或尽量减少匝数。

3.4漏磁通

　　在2.10节已经提到磁通不可能完全耦合所有的线圈（即有漏磁通），线圈的自感可写成：

　　L1=N12（a＋b）和L2=N22(a＋c)

　　首先考虑原边。原边中的aN12项可认为是忽略漏感的理想自感，而bN12项相当于漏感的作用（即漏电感）。所以可在等效电路的理想原边线圈上增加一个串联电感来表示漏磁通的影响，如图13所示。这种论证同样适用于同一变压器的副边线圈。

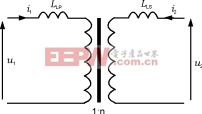
图13漏感

　　漏电感大小与线圈绕制工艺和磁心几何结构有关。

3.5分布电容

　　在实际变压器的绕组中存在寄生电容。最值得注意的是线圈导线和变压器磁心之间以及各绕组之间的寄生电容。电容量的大小由绕组的几何形状、磁心材料的介电常数和它的封装材料等来决定（如在设备中可用环氧树脂密封封装或绕组内部用聚四氟乙烯绝缘）。原、副边电容效应是由线圈匝间的电容引起的，尽管匝和匝之间的电容通常是很小的，因电容串联之和要比并联的小，但作为一个绕组间分布电容的模型，也应在变压器等效电路每一理想线圈两端并联一个集中的电容，如图14所示。

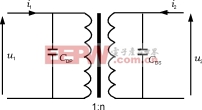
图14分布电容

3.6绕组之间的电容

　　在变压器原边和副边绕组之间的电容（图15中的CWW）。这个电容的大小取决于绕组的几何形状、变压器磁心材料的介电常数和它的封装材料等。通常这个电容和变压器的电感相比是很小的，它的影响只有在工作频率高于变压器的上限截止频率时才起作用。

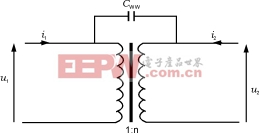
图15绕组之间的电容

3.7综合等效电路

　　综合3.1～3.6节所述的非理想因素，可以得出变压器的一般等效电路,如图16所示。

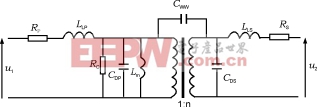
图16变压器的一般等效电路