脉冲变压器的磁学

　　B—磁感应强度（单位：T）

　　H—磁场强度（单位：A/m）

在空气隙中的磁导率μ是一常数（μ=μO=4π×10－7

H/m）。其它材料B－H关系曲线的一般形式如图3所示。初始磁导率μi[1]是磁性材料磁化曲线始端磁导率的极限值，即：2.6B－H曲线

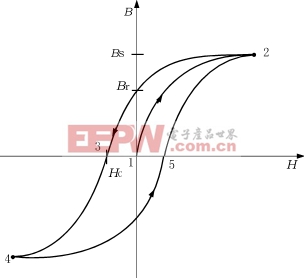
图3B－H曲线

　　图3展示的B－H曲线是一磁滞回线[2]，在B和H的增量很小范围内，磁导率μ可以认为是一常数。

　　如果导磁材料曲线起始部分磁场强度H值增加，则对应的B值就沿着曲线1→曲线2增加。在B和H是零的那一点曲线的斜率称为初始磁导率。当H值增加,到达点2以后，B值就不再随之增加。称此点为饱和点,它对应的B=BS。此时如减小H值，B和H关系曲线的轨迹变为2→3→4。当H减小到零时（2与3点之间），B有一剩余值，B=Br。当H反向后，B又逐渐减小，在点3，B值再次等于零，此时称为矫顽力,H=HC。反向H作用下的点4也是饱和点。如果此时H增加，对应曲线的轨迹是4→5→2。此时曲线不再通过1点。

　　在纯交流电的状态下，B－H曲线每一周期的轨迹都是2→3→4→5→2的环状曲线。

　　B－H曲线的磁滞回线与磁心损耗有联系，磁心损耗与磁滞回线环的面积成正比。

2.7相对磁导率

　　磁性材料的相对磁导率定义如下：

μr=μ/μo(7)

式中μr—材料的相对磁导率

μ—材料的绝对磁导率

μ0—真空磁导率[3]

2.8磁阻

根据图1理想变压器，应用式（4）可写出：

Ni=N1i1－N2i2和∑Hili=Hl=Bl/μ=lΦ/Aμ

磁阻Rm=l/Aμ(H－1)(8)

N1i1=ΦRm＋N2i2(9)

式（9）等式右边表示输出可得到的有效安匝数，要比等式左边的输入安匝数小ΦRm，这一项相当于在磁心内部建立起磁场所需的磁势，称它为磁心的励磁。

　　在理想情况下，当μ→∞Rm→0，则

i1/i2=N2/N1=n(10)

2.9自感

　　线圈的自感是线圈电流所产生的磁场在线圈上所形成的电感。它的定义如下：

e=－Ldi/dt(11)

式中L—自感（单位：H）

　　e—电感上电压（单位：V）

　　t—时间（单位：s）

各种几何形状电感的计算中，如包含有和安掊定律有关的H及I的求和/求积计算时，要求出它的电感量是比较复杂的。举一简单实例，求一环形磁心上理想

线圈的电感（见图4）。

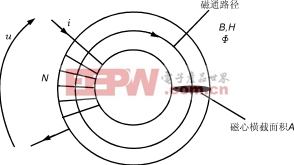
图4环形磁心上的电感

　　从法拉弟定律可得：

u=NdΦ/dt=NAdB/dt，于是

u=NAμdH/dt(12)

　　从安培定律可得：

　　Ni=Hl（13）

由式（12）和（13）可得：　　于是可求出电感为：

L=N2Aμ/l(14)

2.10互感

　　对于变压器和其它耦合线圈还应考虑副边（和其它）线圈对原边线圈所产生磁场的影响。两个线圈之间耦合磁通的影响所导致的电感称之为互感。

　　我们考虑两个线圈在同一个磁心上的情况。在一般情况下，不是所有磁通和所有线圈都耦合，如图5所示。

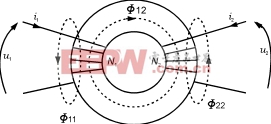
图5耦合线圈

　　按照安培定律可以写出：

Φ12=a(N1i1＋N2i2)

Φ11=bN1i1

Φ22=cN2i2