TR-R2多站雷达系统的近程应用分析与仿真
七、细柱状目标长度估计
雷达发射FMCW波形时，体目标回波频谱将占据一定的带宽，对回波信号作频谱分析则可以提取到此频宽信息.
设细柱状目标的长度为m,接收机Si的接收信号谱宽为Δνi，目标在Si方向的投影为mi，则有如下关系成立
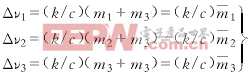(29)
这里，目标投影及频谱宽度均应有正负号，符号的选取由目标相对各雷达站的位置关系及目标的空间取向确定.位置关系取决于几何中心坐标，而空间取向可由目标回波的频谱特性或速度的方向判别.将投影mi以矢量mi表示，其方向由相应雷达站Si——目标视线的方向余弦确定，即
mi=mi［cosαi cosβi cosγi］T (30)
再将细柱状目标以空间矢量M表示，其在三个坐标轴上的投影分量分别为X1，X2，X3，利用矢量关系求得
M=Φ-1δ (31)
式中δ=［m1 m2 m3］T.目标长度的估计式为
(32)
八、目标长度估计性能分析
因各雷达站对频率的测量相互独立，且频率测量误差符合具有相同方差的零均值正态分布，则Δνi是正态分布的.而
i与Δνi是线性关系，因此i正态分布.其概率密度函数为
(33)
式中0i为i的均值.式(29)表明mi与i是线性关系，故mi也符合正态分布.同样式(31)表明Xi与mi也是线性关系，故Xi也符合正态分布.即
(34)
式中，
为Xi的均值，σ2Xi=σ2［k21i+k22i+1/4(kli+k2i-k3i)2］为Xi的方差.根据式(34)可写出X1,X2，X3的联合概率密度函数
(35)
式中H为Xi的协方差矩阵，其元素为
h(i,j)=E［(Xi-X0i)(Xj-X0j)］;
εt=［X01 X02 X03］T
九、计算机仿真结果
选择一种代表性的情况模拟各种参数对系统性能的影响.将三个站分别布在XOY平面内半径为L(称为布站半径)的圆周上，坐标分别为(-L
/2,-L/2,0),(L/2,-L/2,0),(0,L,0).在假定目标始终指向坐标原点的情况下模拟目标数据，分析探测性能.假定目标真实长度为3m，速度500m/s，单站测距均方根误差0.5m，测速均方根误差20m.
1.目标几何中心定位
(1)定位坐标偏移量 图4给出几种不同情况下目标定位坐标偏移量分布，由图看出，当目标高度在200m以下时，坐标估计偏移量较大.目标在200m以上时坐标偏移量已很小，一般可以忽略.同时系统布站半径L越大坐标偏移量越小.
图4 不同情况下定位坐标估计偏移量分布 (2)定位误差的GDOP因子 图5图6分别给出了定位误差的GDOP因子与目标高度及系统布站半径的关系.显然，目标越高定位误差的GDOP因子越小.而增大统布站半径时，GDOP因子越小.而增大统布站半径时，GDOP因子先是减小，然后又增大，这种变化不是单调的.当考虑中心附近2km见方的近程区域时，L=2km的情况为最好. |
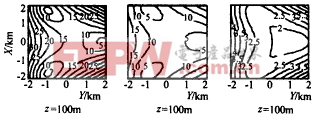
图5 高度不同时的GDOP曲线(L=2km)
相关推荐技术专区 |
评论