分数阶Fourier变换应用于水声通信及其FPGA实现
——
FRFT在信号处理和通信等领域已有许多应用[10]。本文利用FRFT适用于处理Chirp类信号的优势，初步研究了基于FRFT的调制解调技术。
根据FRFT的逆变换公式：
可知，信号x(t)的FRFT 可以理解为x(t)在以其逆变换核
为基的函数空间上的展开，而此核是u域上的一组正交Chirp基。因此一个Chirp信号在适当的u域中对于特定的Chirp信号具有最好的能量聚集特性。用FRFT实现线性调频信号的参数检测和估计可通过旋转角α对变量进行扫描，通过对信号进行快速的FRFT，再以(α，u)的二维平面中进行峰值搜索，即可较准确估计被检测信号的幅度、初始相位、起始频率等参数值。
对于一组调频斜率相同但中心频率不同的线性调频信号，可以根据不同的冲击函数找到对应的原信号的频率，从而还原出原信息。例如可将数字信息(00，01，10，11)调制到四组斜率相同但中心频率不同的线性调频信号上。在接收端将接收数据进行FRFT，之后将变换后的数据在u域进行峰值位置搜索，找到其最大值进而确定出原线性调频信号的中心频率，从而还原出原信息，上述过程如图1所示。
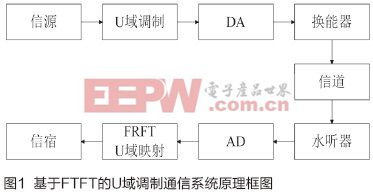
FRFT是线性变换，由于它具有信号能量聚焦性，而噪声却不会聚焦，使其在具有加性噪声的多分量情况下更具优势。为了更好地说明它的优点，进行了计算机对比仿真研究。
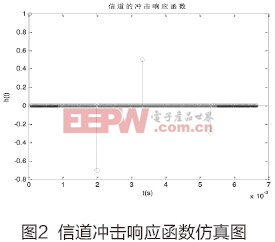
仿真条件：信噪比从-20dB至10dB，仿真信道如图2所示。
fpga相关文章:fpga是什么
数字通信相关文章:数字通信原理
通信相关文章:通信原理
评论