频率响应法--奈奎斯特稳定判据
加入技术交流群
＝2时，
刚好经过（－1，j0），系统处于临界稳定状态；当
＝4时，
包围（－1，j0）点，所以闭环系统是不稳定的。可见，时滞时间的增大，对控制系统的稳定和性能都是极为不利的。 |
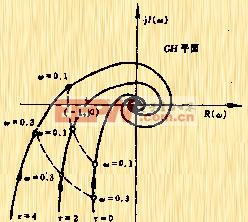| 图5－47 |
5.4.4 奈氏稳定判据在对数坐标图上的应用
与奈氏图的绘制相比，开环对数频率特性的绘制更为简单、方便，因而研究开环对数频率特性形式的奈氏稳定判据是有实际意义的。注意到开环系统的奈氏图与相应的对数坐标图之间有着下列的对应关系：
1）GH平面上单位圆的圆周与对数坐标图上的0dB线相对应，单位圆的外部对应于
，单位圆的内部对应于
。
2）GH平面上的负实轴与对数坐标图上的
线相对应。
 |
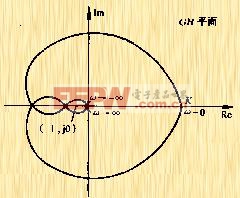| 图5－48a 奈氏图上正、负穿越 |
 |
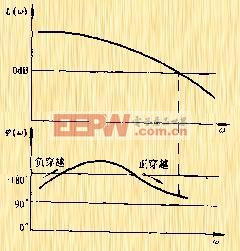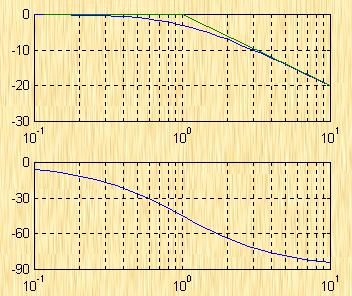
| 图5－48b 伯德图上正、负穿越示 |
如果
曲线以逆时针方向包围（－1，j0）点一周，则此曲线必然由上向下穿越负实轴的
线段一次。由于这种穿越使相角增大，故称为正穿越，其次数用
表示。反这，若
曲线按顺时针方向包围（－1，j0）点一周，则此曲线将由下向上穿越负实轴的
线段一次。由于这种穿越使相角减小，故称为负穿越，其次数用
表示。图5－48a所示的为正负穿越数各一次的图形。显然，对应于图5－48a上的正负穿越在伯德图上表现为：在
的频域内，当
增加时，相频曲线
由下而上（负穿越）和由上而下（正穿越）穿过
线各一次，如图5－48b所示。
不难看出，在极坐标图上
曲线对于（－1，j0）点的包围圈数N与其相频特性曲线
在对数坐标图上的负，正穿越数之差相等。即有
 |
|
式中
， 为在 
频率范围内
的负穿越数；
为在
频率范围内
的正穿越数。这样，式（5－44）便可改写为
 |
|
应用上式，就可得到对数频率特性形式的奈奎斯特判据：闭环系统稳定的充要条件是，当
变化时，在
频率范围内，相率特性
穿越
线的次数（正、负穿越数之差）为
。
在使用对数频率特性的奈氏稳定判据时，应注意如下两点：
（1） 判据中的频率范围是
，而非如前述的 
；
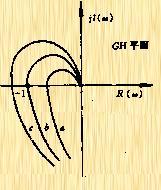
（2） 若P为奇数，则意味着开环系统并未产生真正的穿越，即相频特性的起点在负半轴
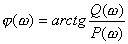
评论