频率响应法--奈奎斯特稳定判据
加入技术交流群
曲线以顺时针方向包围（-1，j0）点旋转两周，这意味着有两个闭环极点位于s右半平面上，该闭环系统是不稳定的。 |
2、利用奈氏判据确定系统的参数稳定范围
如果系统中的某个参数或若干个参数是可以变化的，为使系统稳定，可利用奈氏判据来确定系统的参数稳定范围，即根据奈氏曲线是否通过（－1，j0）点的条件来选定参数。下面以例说明之。
例5－8 试用奈氏判据确定该闭环系统稳定的K值范围。
已知一单位反馈系统的开环传递函数为
 |
试用奈氏判据确定该闭环系统稳定的K值范围。
解 该系统是一个非最相位系统，其开环系统幅频和相频特性的表达式分别为
 |
 |
 |
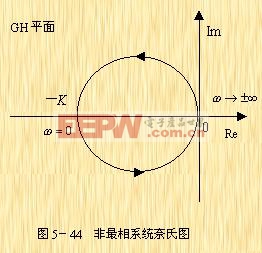和惯性环节一样，它的奈氏图也是一个圆，如图5－44所示。由于系统的P＝1，当ω由
变化时，
曲线如按逆时针方向围绕（－1，j0）点旋转一周，即N＝－1，则Z＝1－1＝0，表示闭环系统是稳定的。由图5－44可见，系统稳定的条件是K＞1。
3、具有时滞环节的稳定性分析
由于时滞系统的开环传递函数中有着
的环节，其闭环特征方程为一超越方程，因而劳斯稳定判据就不适用了。但是，奈氏稳定判据却能较方便地用于对这类系统稳定性的判别。
设含有时滞环节的开环系统的传递如下：
 |
|
式中， 
为时滞时间常数。将上式改写成：
 |
|
其中
 |
|
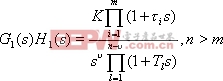不含时滞环节的传递函数。相应地，开环系统的幅频特性和相频特性为：
 |
|
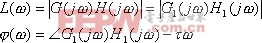上式表明，当
时，相对于
，
的幅值没有变化，而相角则在每个
上顺时针多转动了
。
由于实际的控制系统中，
，因此当
时，
的模趋于零，因而
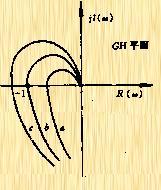
随
以螺旋形趋于原点，并且与GH平面的负半轴相交无穷点，如图5－45。因此为使系统稳定，奈氏曲线与负实轴相交点必须位于（－1，j0）的左边。
 |
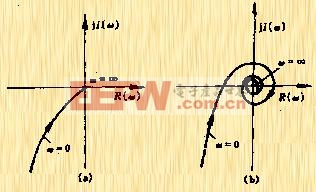| 图5-45 |
例5－9 试分析滞后时间 对系统稳定性的影响。
设一时滞控制系统如图5－46所示。已知图中的 
，试分析滞后时间
对系统稳定性的影响。
 |
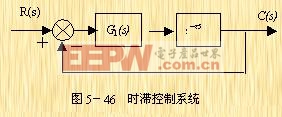解 系统的开环传递函数为
 |
|
取
值分别为0,2，4，图5－47示出了式（5－51）在不同 
值时的奈氏曲线。由图可见，当滞后时间
为零时，系统相当于无时滞环节，
不包围（－1，j0）,所以闭环
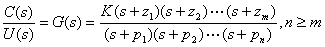
评论