频率响应法--奈奎斯特稳定判据
加入技术交流群
，因为辐角原理只适用于奈氏轨线 不通过
的奇点。为此，可对图5－37所示的奈氏轨线作些修改，使其沿着半径为
的半圆绕过虚轴上的所有极点。假设开环系统在坐标原点处有其极点，则对应的奈氏途径要修改为如图5－40所示。比较图5－40与图5－37可以发现，它们的区别在于图5－40中多了一个半径为无穷小的半圆
部分，其余两者完全相同。因此，只需要研究图5－40中的
部分在GH平面上的映射。 |
设系统的开环传递函数
 |
|
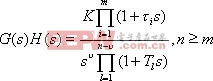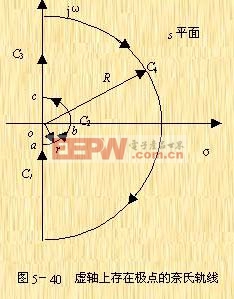
在
部分上，令
，其中
，代入上式得
 |
|
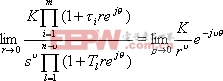当s按逆时针方向沿着
由点a移动到c时，由式（5－46）可求得其在GH平面上的映射曲线：
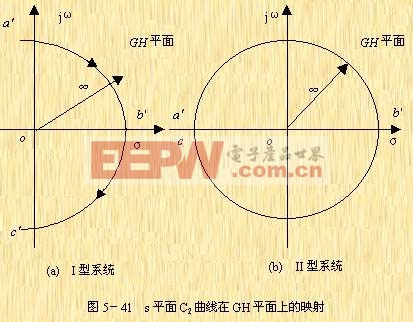
对于
的I型系统，
部分在GH平面上的映射曲线为一个半径为无穷大的半圆，如图5－41a所示。图中点
、
和 
分别为
半圆上点a、b和c的映射点。
对于
的Ⅱ型系统， 部分在GH平面上的映射曲线是一个半径为无穷大的半圆，如图5－41b所示。
 |
把上述
部分在GH平面上的映射曲线和
的奈氏曲线在
和
处相连接，就组成了一条封闭曲线。此时，又可应用奈奎斯特稳定判据了。
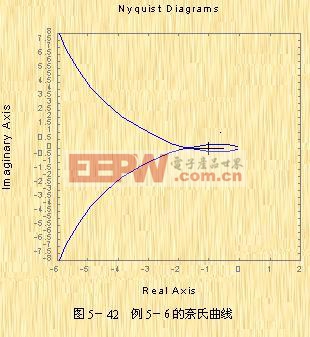
例5－6 试判别该系统的稳定性。
反馈控制系统开环传函数为
 |
试判别该系统的稳定性。
解：由于该系统为I型系统，它在坐标原点处有一个开环极点，因而在s上所取的奈氏轨线应如图5－40所示。该图的
部分在GH平面上的映射曲线为一半径为无穷大的半圆，若将它与图5－42的奈氏曲线
相连接，则有N＝2，而系统的P＝0，因而Z＝2，即闭环系统是不稳定的，且有两个闭环极点位于s的右半平面。
 |
例5－7 试分析时间常数的相对大小对系统稳定性的影响并画出它们所对应的奈氏图。
已知系统的开环传递函数为
 |
试分析时间常数
和
的相对大小对系统稳定性的影响，并画出它们所对应的奈氏图。
解 由开环传递函数得
 |
 |
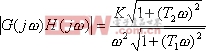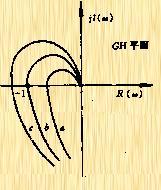
根据以上两式，作出在
，
和
三种情况下的
曲线，如图5-43所示。当 时， 曲线不包围（－1，j0）点，因而闭环系统稳定的。当
时，
曲线通过（－1，j0）点，说明闭环极点位于
轴上，相应的系统为不稳定的。当
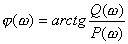
评论