频率响应法--奈奎斯特稳定判据
加入技术交流群
的一个零点－
，
的其余零点和极点均位于闭合曲线
之外。当点s沿着闭合曲线 走了一周时，向量
的相角变化了
，其余各向量的相角变化都为
。这表示在
平面上的映射曲线按顺时针方向围绕着坐标原点旋转一周，如图5－36所示。由此推论，若s平面上的闭合曲线
以顺时针方向包围
的z个零点，则在 平面上的映射曲线
将按顺时针方向围绕着坐标原点旋转z周。如果s平面上的闭合曲线
按顺时针方向围绕着
的一个极点
旋转一周，则向量
的相角变化了
。由式（5－42）可知，
的相角变化了
。这表示
平面上的映射曲线
按逆时针方向围绕其坐标原点一周。由此推广到一般，若s平面上的闭合曲线
按顺时针方向围绕着
的p个极点旋转一周，则其在 平面上的映射曲线 按逆时针方向围绕着坐标原点旋转p周。
综上所述，可得到如下的辐角原理。
辐角原理 设除了有限个奇点外， 是一个解析函数。如果s平面上的闭合曲线 以顺时针方向包围了 的Z个零点和P个极点，且此曲线不通过 的任何极点和零点，则其在 平面上的映射曲线 将围绕着坐标原点旋转N周，其中
。若
，表示曲线
以顺时针方向围绕；若
，则表示曲线
以逆时针方向围绕。
 |
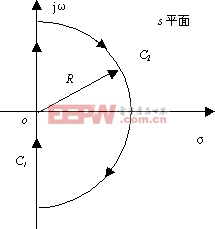| 图5－37 右半平面的封闭曲线 |
如果闭环系统是稳定的，则其特征方程式的根，即
所有的零点均位于s的左半平面。为了判别系统的稳定性，检验 是否有零点在s的右半平面上即可。为此，在s平面上所取的闭合曲线
应包含s的整个右半平面，如图5-37所示。这样，如果
有零点或极点在s的右半平面上，则它们必被此曲线所包围。这一闭合曲线称为奈奎斯特轨线，它是由
轴表示的
部分和半径为无穷大的半圆
部分组成。即s按顺时针方向沿着
由
运动到
，尔后沿着半径为无穷大的半圆
由
运动到
，其中
。
由于
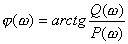
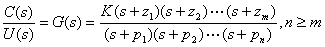
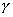
评论