频率响应法--奈奎斯特稳定判据
![]() =常数
=常数
这说明当s沿着半径为无穷大的半圆变化时,函数![]() 始终是一常数。由此,
始终是一常数。由此,![]() 平面上的映射曲线
平面上的映射曲线![]() 是否包围坐标原点,只取决于奈氏轨线中
是否包围坐标原点,只取决于奈氏轨线中![]() 部分的映射,即由
部分的映射,即由![]() 轴的映射曲线来表征。
轴的映射曲线来表征。
设在 ![]() 轴上不存在
轴上不存在![]() 的极点和零点,则当s沿着
的极点和零点,则当s沿着![]() 轴由
轴由 ![]() 运动到
运动到![]() 时,在
时,在![]() 平面上的映射曲线
平面上的映射曲线![]() 为
为
|
设闭合曲线![]() 以顺时针方向包围了
以顺时针方向包围了![]() 的z个零点和p个极点,由辐角原理可知,在
的z个零点和p个极点,由辐角原理可知,在![]() 平面上的映射曲线
平面上的映射曲线![]() 将按顺时针方向围绕着坐标原点旋转N周,其中
将按顺时针方向围绕着坐标原点旋转N周,其中
|
由于
因而映射曲线![]() 对其坐标原点的围绕相当于开环频率特征曲线
对其坐标原点的围绕相当于开环频率特征曲线![]() 对GH平面上的(-1,j0)点的围绕,图5-38示出了奈氏曲线映射在这两个平面上的位置。
对GH平面上的(-1,j0)点的围绕,图5-38示出了奈氏曲线映射在这两个平面上的位置。
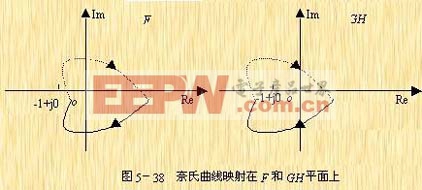 |
通过上述分析可知,闭环系统的稳定性可通过其开环频率响应![]() 曲线对(-1,j0)点的包围与否来判别,这就是下述的奈奎斯特稳定判据。
曲线对(-1,j0)点的包围与否来判别,这就是下述的奈奎斯特稳定判据。
(1) 如果开环系统是稳定的,即P=0,则闭环系统稳定的充要条件是![]() 曲线不包围(-1,j0)点。
曲线不包围(-1,j0)点。
(2) 如果开环系统不稳定,且已知有P个开环极点在s的右半平面,则闭环系统稳定的充要条件是![]() 曲线按逆时针方向围绕(-1,j0)点旋转P周。
曲线按逆时针方向围绕(-1,j0)点旋转P周。
综上,应用奈氏判据判别闭环系统的稳定性的具体步骤为:
(1)首先要确定开环系统是否稳定,若不稳定,则P为多少?
(2)作出奈氏曲线![]() 。具体作图时可先画出
。具体作图时可先画出![]() 从0到
从0到![]() 的一段曲线,然后以实轴为对称轴,画出
的一段曲线,然后以实轴为对称轴,画出![]() 从0到
从0到![]() 的另一段曲线,从而得到完整的奈氏曲线。
的另一段曲线,从而得到完整的奈氏曲线。
(3)计算奈氏曲线![]() 对点(-1,j0)按顺时针方向的包围圈数N。
对点(-1,j0)按顺时针方向的包围圈数N。
(4)根据辐角原理确定Z是否为零。如果Z=0,表示.闭环系统稳定;反之,![]() ,表示该闭环系统不稳定。Z的数值反映了闭环特征方程式的根在s右半平面上的个数。
,表示该闭环系统不稳定。Z的数值反映了闭环特征方程式的根在s右半平面上的个数。
例 5-5 试用奈氏判据判别闭环系统的稳定性。
系统的开环传递函数为
试用奈氏判据判别闭环系统的稳定性。
解:当ω由![]() 变化时,
变化时,![]() 曲线如图5-39所示。因为
曲线如图5-39所示。因为![]() 的开环极点为-0.5,-1,-2,在s的右半平面上没有任何极点,即P=0,由图5-39可知,由于奈氏曲线不包围(-1,j0)这点,因此N=0,则Z=N+P=0。这表示该闭环系统是稳定的。
的开环极点为-0.5,-1,-2,在s的右半平面上没有任何极点,即P=0,由图5-39可知,由于奈氏曲线不包围(-1,j0)这点,因此N=0,则Z=N+P=0。这表示该闭环系统是稳定的。
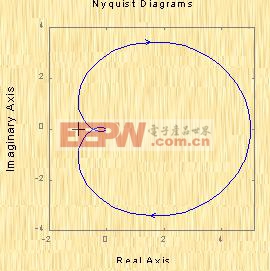 |
| 图5-39 |
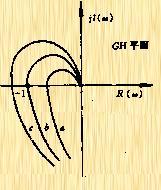
5.4.3 奈奎斯特稳定性判据的进一步说明
1、开环极点位于虚轴的情况
如果![]() 在虚轴上存在极点,那么就不能
在虚轴上存在极点,那么就不能



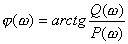


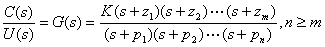
评论