差分编码在水声电子通信中的应用研究

3.仿真统计结论

使用编码方式(1)和(2)仿真统计了持续3 0 s的时间序列记录，其中m1的取值范围是{1,2,3,4},m2的取值范围是{m1,1,2,3,4}.在不同信噪比条件下计算误比特率(BER)，信噪比取值范围为{-40,-30,…，10},计算SNR(单位：dB)的公式如下：

SNR=-20log10(r0σ ) (5)

其中r0是固定信源到固定接收器处的参考距离，σ 是附加的复杂高斯噪声标准差。

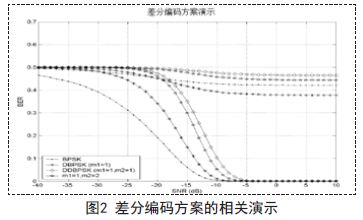
如图2所示，BER与SNR的关系用八条曲线描绘，使用四种差分编码方式共分两组：

B P S K (未编码);D B P S K (二阶m l - H I M ,m1=1);(三阶ml-HIM,m1=1,m2=1);DDBPSK(三阶ml-HIM,m1=1,m2=2)。其中四组曲线在接收器活动范围内对应的各种信噪比条件下反映的误比特率均高于0.3;而另外四组在固定接收器处高信噪比条件下的误比特率接近0的曲线是参考曲线。

4.接收器问题讨论

从图2我们即可发现，没有一个差分编码方式可以解决接收器运动问题，所有差分编码方式在所有信噪比条件下的误比特率都不小于0.38.因此，即使接收器只有轻微的波浪状运动，ml-HIM也无法较好的抵消接收信号(在运动的接收器处得到的有噪声的时间序列)与参考时间序列(在固定位置均值接收器处得到的无噪声时间序列，去掉直接路径射线)之间由于失配造成的误码。

通过观察得知：最佳的结果是完全没有进行差分编码(BPSK曲线)，并且DBPSK在所有信噪比条件下的误比特率都比BPSK要高。同样，DDBPSK在所有信噪比条件下的误比特率都比DBPSK要高。通过使用广义差分编码的概念，选择DDBPSK中除m1=1,m2=1外的时延，能够得到比DDBPSK要好的结果。事实上，如图2所示，在接收器静止时，m1=1,m2=2时的曲线就在DBPSK和DDBPSK曲线之间。

然而，当允许接收器运动时，一个不同的结果出现了。图2中靠上的4条曲线很清晰的证明了，即使是理想信道条件，也不能够完全抵消差分编码造成的信号失真。可以注意到最好的表现来自普通BPSK与DBPSK编码，并且这也是唯一比完全不编码(BPSK)略好的编码方式。

我们还注意到，DDBPSK的表现最差，仅仅比m1=1,m2=2时使用广义三阶ml-HIM得到的结果好一点。这和Gini和Giannakis在不同的时延下观察到的结果是一致的，而不是传统上的认为DDBPSK能比DBPSK更好的抵消运动引起的信号失真。

或许广义差分编码方法更适合认为操纵运动的潜艇，这样潜艇产生不规则运动会少一些潜艇在运动中产生的扰动较小。在绝大部分容器中进行仿真时，波浪一直出现，无论如何总会存在持续几秒的，波长至少半米的波浪干扰。相反，降低载波频率可以预期提供更好的表现，因为波长会长一些。假设载波频率为15kHz,水中的波长就为0.1m,因此接收器运动产生的扰动会比很多波长要高。在载波频率为1.5kHz时，波长为1m,同样的扰动现在也就一个信号波长左右。

5.结束语

通过仿真，展示了在文中假设的条件下，广义差分编码技术并未展示出应有的增益。为改进广义差分编码方法的表现也许需要混合信道编码，或者某种判决反馈均衡器。