如何使用一个DSP block实现4个11位浮点型数据乘法运算

　　概述

　　随着深度学习的发展，为了解决更加抽象，更加复杂的学习问题，深度学习的网络规模在不断的增加，计算和数据的复杂也随之剧增。INTEL FPGA具有高性能，可编程，低功耗等特点，为AI应用加速提供了一种灵活、确定的低延迟、高通量、节能的解决方案。Arria10是INTELFPGA第一代集成IEEE754标准单精度硬浮点DSP block，可以为高复杂度的深度学习算法提供高精度，高能效的乘法运算。

　　深度学习算法复杂度高，需要进行大量的乘法运算，如实现一个卷积核为5*5的特征提取，需要进行25*25次乘法运算，而随着特征提取量的增加，乘法运算也将成倍的增长。因此乘法器资源是实现深度学习算法的重要评估资源，本文主要介绍如何基于Arria10的一个18*18的乘法器实现两个11*11的浮点mini-fp运算，从而4倍提高DSP block资源。

　　原理分析

　　Arria10可变精度的DSP Block支持配置为两个18*18或者18*19定点乘法器，进行18*18乘法运算时，如图1所示，将输入拆分为低6位，中6位，高6位，进行运算分析。

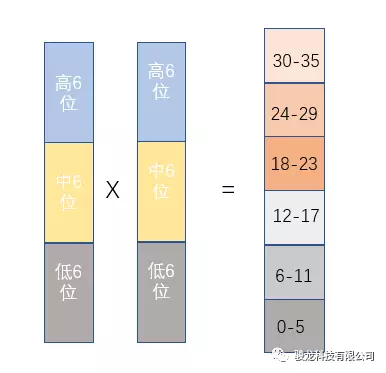
　　图1 18*18乘法器运算

　　则对应的运算结果如下表所示：

　　将中6位输入全设为0，则可以得到对应的输出结果如下表所示：

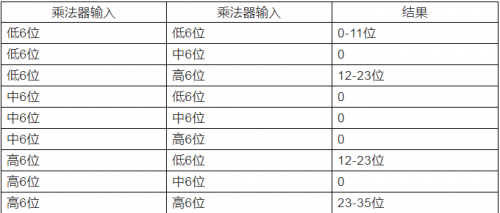
　　当高6位及低6位为带符号位的输入数据时，进行符号位提取，则剩余的实际数据有效位为5位，因此低6位*高6位及高6位*低6位的乘法结果最高有效位均为10位，进行两个结果的加法运算，可以保证结果在12-23位以内，不会对高6位*高6位乘法结果造成影响。因此Arria1018*18的乘法器支持进行符号位提取后的两个6*6的乘法运算，图2是对应的仿真结果，乘法结果对应延时2个时钟周期。

　　图2 modelsim 仿真结果

　　浮点型数据如图3所示，包含符号位S，指数位E及尾数位M。

　　图3 浮点型数据组合

　　进行浮点型数据乘法运算，如图4所示。

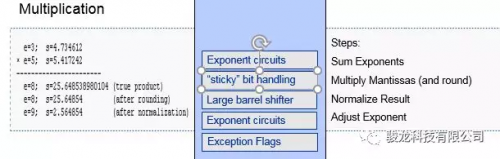
　　图4 浮点型数据乘法

　　需要进行指数相加，尾数相乘，乘法结果取整及指数的调整。11位的浮点型数据尾数及指数各占5位，因此进行乘法运算仅需要进行包含符号位6位的数据相乘及对应的处理即可。Arria10的DSPblock可支持配置为2个18*18乘法器，而一个18*18的乘法器可以实现两个6*6的乘法运算，因此一个DSPblock可以实现4个11位浮点型数据mini-FP的乘法运算。