基于Matlab/Simulink/Dsp的厢式半挂车实时道路仿真

　　将微分方程转换成状态空间下的方程，即

　　式中x是半挂车的状态向量，12个分量分别表示6个自由度处的位移和速度；u是输入向量，表示车辆处的路面位移激励；y为输出向量，设置为6个自由度处的位移和速度；A为系统矩阵；C为输出矩阵，设置为一个12阶的单位矩阵；D为控制矩阵，由于没有直接输入对象，设置其为3×12阶的O矩阵。

　　三、仿真模型

　　建立的微分方程及状态方程要进行多次计算并对结果进行各项分析处理，工作量非常大。用Mat2lab所具有的功能，将其转化到Matlab/Simulink/Dsp环境下，从而进行直观有效的分析。

　　在 Matlab/Simulink环境下，一般用基本方框图的数学运算关系连接系统的搭建。考虑到本模型状态方程的特殊性，采用直接应用状态方程模块的方法进行仿真，只需将微分方程的参数代入，设置并添加必要的激励和输出显示等环节即可仿真。为了体现计算的实时性，多数结果数据和曲线可以直接从实时仿真模型中看到，而无需再处理，具有很好的实时性。

　　为了便于与试验对比，以验证模型的正确性，将簧上质量的垂直振动和纵向角振动转化为前后轴上方底板处的垂直振动，同时对加速度信号求自功率谱密度及加速度均方根值，以便于研究分析。由于模型较大，建立了几个子系统。

　　（一）时域输入部分

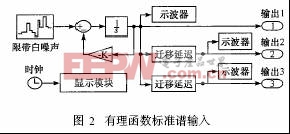
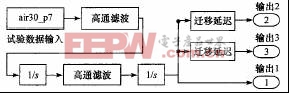
　　用于随机路面输入的信号可以用两种方法获得，一种是根据有理函数标准谱的输入方法模拟时域信号，另一种是直接利用获得的道路时间历程信号。图2、图3中输出 1、输出2和输出3分别作为牵引销处、副车架前轴、副车架后轴处的时域输入。两种不同来源的信号输出模块的内部处理结构分别如图2、图3所示。

　　实测得到的是加速度时间历程，需要进行二次积分并用高通滤波将趋势消除，才能取得随机位移。

　　滤波边界频率取0.5～1.0Hz，能够获得很好的效果。

　　（二）核心计算部分

　　核心计算部分模型如图4所示。

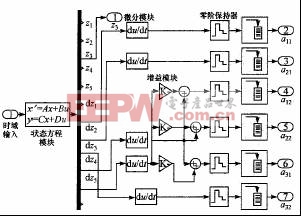
图4 核心计算部分

为了获得加速度输出信息，对输出的速度进行微分计算，并根据几何关系换算对应位置的量值。