基于FPGA的RBF神经网络的硬件实现
2．3 隐层非线性函数映射的实现
RBF神经网络隐层中的映射函数为高斯函数，为非线性函数。而非线性函数在硬件上实现往往比较复杂，难度较大。通常实际工程中采用查表法或迭代法来近似模拟这些非线性函数，查表法较迭代法虽在结构和运算复杂度上有明显降低，但在精度上也会明显降低。若要提高精度，只能增加表的大小，但增加表的大小，直接带来的影响就是会加大存储空间和降低查表效率，所以，在FPGA上采用何种方法实现高斯函数的存储达到精度和效率之间的平衡就至关重要。
高斯函数表达式为
其中，
可以看作是方差为1的高斯函数，而当方差固定时，高斯函数的形状不会发生变化，只是位置上会发生平移，此时我们可以采用查表法来解决该部分的非线性映射，为进一步提高查表效率、压缩ROM表的存储空间，在这里采用STAM(Symmetric Table Loo kup Addition Method)算法实现数据的非线性存储；另外，
部分中心固定，而且
维持在一定范围，可以采用CORDIC迭代法来实现该部分的函数计算。2．3．1 STAM算法
STAM算法的主体思想是先产生系数，然后利用系数的对称性减小ROM表的大小。在该算法中先把输入X分为m+1个部分：x0，x1，…，xm。则f(x)可以近似为
该种方法虽然在某种程度上使得查找表的数量增加了，但每个表的大小却大大减小了，整体上查找表还是减少了，效率上也相应提高了。
式(13)构造的查找表a0(x0，x1)，其输入值的位数为n0+n1。式(14)所构造的其余m-1个查找表ai-1(x0，xi)，由于δi被定义为xi的取值区间的中间点，故查找表中的系数值具有对称性，即ai-1(x0，xi)与ai-1(x0，2δi-xi)互为补码，其输入值的位数可以减为n0+n1-1，从而使这m-1个查找表的存储空间节省了一半。
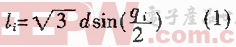
评论