基于FPGA的高阶FIR抽取滤波器有效实现结构
为进一步利用网络结构等效性,可以将抽取与各支路滤波器进行等效变换,从而得到如图2(b)所示更为有效的多相抽取滤波结构图,其中
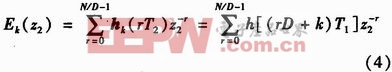
相对图1所示的直接实现结构,图2(b)所示的高效实现结构具有如下两个特点:(1)各支路滤波器输入信号速率为原输入信号速率的1/D,从而可以使得各支路滤波器工作在较低的速率上。(2)各支路滤波器系数个数为原滤波器系数个数的1/D。因此,相比图1,图2(b)所示的滤波器结构具有更高的运算效率。
2 FIR抽取滤波器的多相结构实现
采用多相结构实现抽取滤波器的基本思想是将输入信号进行相应延迟和降采样后,分别送至D个通道进行滤波,然后将每一支路滤波后的数据相加,得到最终输出结果。如2(b)所示,降采样后进行第一个滤波通道的信号数据为…,x(0T1),x(DT1),x(2DT1),…,进入第二个滤波通道的信号数据为…,x(-1T1),x((D-1)T1),x((2D-1)T1)…,进入最后一个通道的数据为…,x((-D+1)T1),x(1T1),x((2D+1)T1),…,等等。结合上述特点,在FPGA进行实现时,可以将延迟和降采样结合在一起,采用图3(a)所示的实现结构进行抽取滤波。该结构中包括3个模块:(1)串并转换,将输入数据转换成D路并行信号。(2)多相滤波模块,将得到的D路并行信号分别进行滤波,每一路所采用的滤波器为原滤波器相应的多相分量。(3)加法模块,该模块将上述得到D路滤波后的数据相加得到最终的一路输出信号。本文引用地址:https://www.eepw.com.cn/article/189742.htm
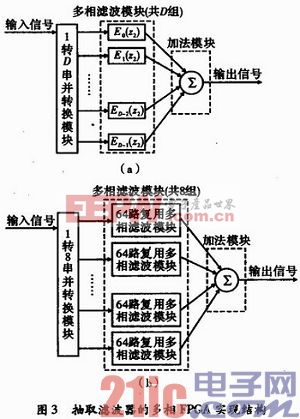
但随着降采样率D的增加,相应的所需要的FPGA资源也急剧增加。例如,当D=512时,图3(a)对应的实现结构需要至少512个乘法器,这在实际中难以满足要求。由于D较大时,各路滤波器工作时钟频率却很低。为了更少地使用乘法器资源,同时提高系统的工作效率,在图3(a)的基础上可以进一步优化结构。
改进后的实现结构核心思想:可以将图3(a)中D个通道分成L组,每组包括D/L通道,每一组采用分时复用方法进行实现滤波。同时,针对每一组滤波,进一步提高工作时钟频率,采用更少的乘法器实现抽取滤波器。下面将结合一个具体的设计要求给出更适合FPGA实现的多相滤波结构。该系统指标如下:输入数据速率(或系统时钟f1=204.8 MHz;降采样率D=512;滤波器阶数N=4 096;FPGA芯片Xilinx公司的VirtexⅣ芯片。
如果采用图1所示的直接型结构至少需要4 096个乘法器,采用图2(b)所示的多相滤波结构也至少需要512个乘法器,均无法满足指标要求。为此,可以采用复用方法进行实现。根据技术指标要求,原滤波器的多相分量含有N/D=8个系数,同时,每一路速率为fk=f1/D=0.4 MHz,因此,可以将D路滤波通道分成=8组,每组D/L=64路信号复用,同时滤波时乘法器进一步复用,则每一个滤波器工作频率为fl=fk×64 ×8=f1=204.8 MHz。图3(b)给出了优化后的抽取滤波器多相实现结构。由于每组多相滤波模块中同时完成64路的滤波功能,同时滤波器实现过程对成绩和操作也进行复用,每一组多相滤波模块只需1个乘法器,整个系统共需8个乘法器,大幅节约了乘法器资源。实际也可以根据不同的系统指标要求,针对不同的FPGA芯片性能,设置不同的复用路数和滤波器工作频率,使整个系统资源和性能均满足要求。















评论