RTN的SRAM误操作进行观测并模拟的方法简介

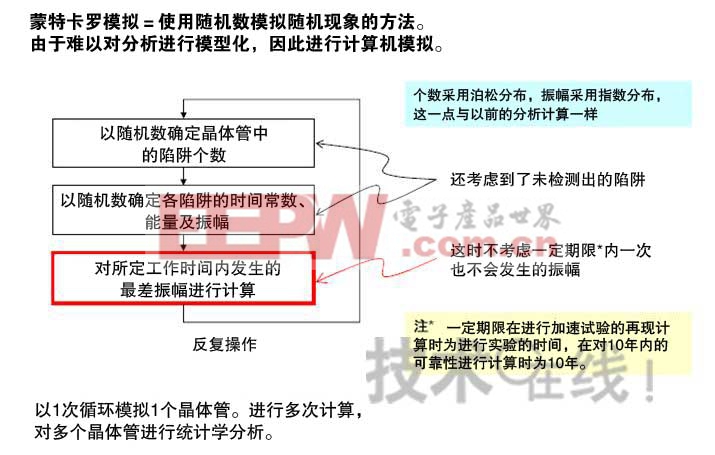
　　此次瑞萨开发了根据陷阱个数、振幅（陷阱引起的特性变动的幅度）及时间常数（捕获和释放电荷的时间间隔）的统计学分布，以蒙特卡罗法对一定时间（比如想保证的产品寿命）内晶体管及电路所产生的特性变动的最大值进行计算的方法（图5）。将以往RTN分析式未考虑的陷阱时间常数和能量作为参数进行了导入。该计算方法不进行严密的电路模拟，只进行概率的计算和振幅的加算。因此，可在实用时间内进行模拟。

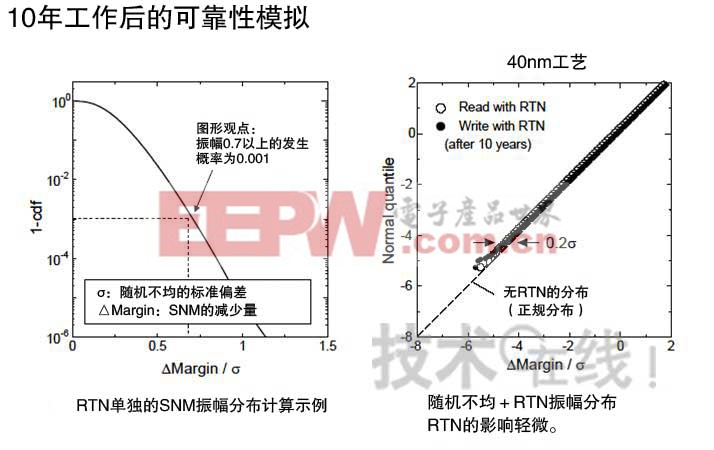
　　该公司为了获得SRAM中RTN所致误操作的发生概率，对6个晶体管构成的组件使用了此次了模拟方法，并根据结果算出了作为SRAM工作稳定性指标的SNM（Static Noise Margin）的变化量。对40nm工艺SRAM进行该变化量的计算后表明，在该工艺中，与杂质不均相比，RTN的影响较为轻微（图6）。

　　从（3）来看，在模拟中体现加速试验的结果以提高精度的手段对于将此次的方法应用于实际的芯片十分重要。这源于各晶体管中存在的陷阱个数、振幅及时间常数等无法通过测定手段来完全掌握。

　　此次的模拟方法，其计算结果会因为作为参数的陷阱时间常数和能量存在分布如何进行假设，以及计算中将其纳入考虑的范围有多大而发生变化。因此，瑞萨以提高模拟精度为目标，开发了使加速试验结果在模拟参数的设定中得到体现的方法。具体而言，就是从加速试验开始考虑SRAM的故障bit数是以何种趋势随着工作次数而增加的，并以能够在模拟中再现这种趋势为目的，修正与陷阱时间常数和能量存在分布相关的假设。