三电平逆变器中点电压平衡的电压空间矢量控制原理及算法

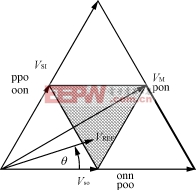
图4 中部小三角形区域电压合成

将式（7）带入式（6）中解得：

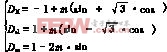（8）

因此，该区域的中线电流可表示为：

iNP=DM·ib＋(mso·Dso·ia＋ms1·Ds1·ic)（9）

式中：mso和ms1为短矢量的调制度。

式（5）与式（9）相比可知，在式（9）中由于存在两个可以调节的短矢量，因此在该区域更有利于中点电压的平衡。

图5为内部小三角形区域参考电压矢量合成图。

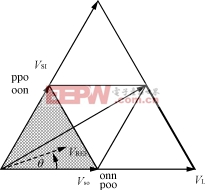
图5 内部小三角形区域电压合成

该区的合成参考电压可表示为：

VREF=DsoVso＋Ds1Vs1＋DoVo（10）

式中：Vo为零矢量电压。

因此根据平行四边形法则，它的占空比为：

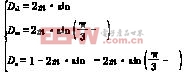（11）

中线电流为：

iNP=mso·Dso·ia＋ms1·Ds1·ic（12）

从式（12）可以看到，中线电流只含可以调制的短矢量，而不含不可调制的中矢量。所以内部区域的参考电压矢量更有利于中线电流的调节，同时有利于中点电压的平衡。但是，它的电压矢量幅值很小，电压利用率不高，该区域只适用于刚起动或瞬态时。

总之，当电压矢量旋转时，稳定运行时，电压矢量只可能在Ⅰ和Ⅱ区域合成。改变ω可以调节输出频率；改变各占空比D可以调节输出电压大小并且通过短矢量占空比调节还实现了中点电压平衡。

4 仿真实验

依据上述关于中点电压平衡的电压空间矢量算法以及三相多电平电压空间矢量快速算法理论[4]，用Matlab对箝位二极管式三相三电平电压型逆变器进行了仿真实验。其中Vdc=200V，采样频率fs=600Hz,调制度m=0.92。各相输出接有R－L负载,输出各相电压仿真波形如图6所示，其中波形Vo是输入电容两端电压之差，即平衡电压波形,输出频率为fo=50Hz。从实验表明，以上的基于电压空间矢量的电压平衡算法是可行的，中点电压可以达到一定范围的平衡。通过三电平的采用，它的输出相电压波形将更近似于正弦波，在相同开关频率条件下，大大降低了谐波污染。

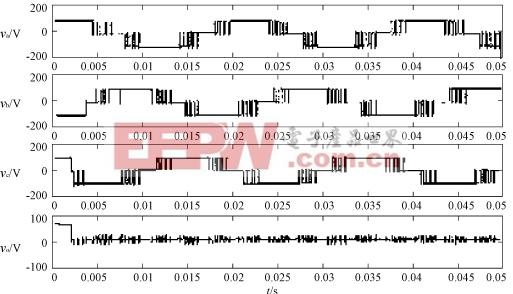
图6 三电平逆变器仿真实验电压波形

5 结语

将电压空间矢量与三电平逆变器相结合，可以集二者优点，同时调节了中点电压的平衡，这样便解决了多电平输入母线电压的不平衡问题。特别是在利用数字信号处理（DSP）的控制中，该方法算法简单，实现容易，具有明显的优势。本文结合了电压空间矢量快速算法，给出了三相三电平逆变器的仿真结果，进一步证明了它的可行性。