移相全桥DC/DC变换器动态建模研究

.

.

移相全桥DC/DC变换器动态建模研究

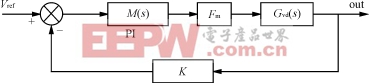
图6系统闭环结构框图

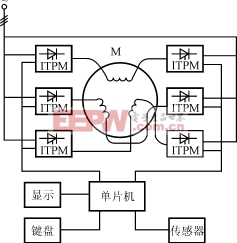
图8负载变化时的输出电压波形

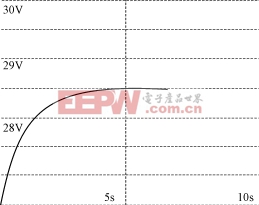
图7输出电压波形

K为反馈放大系数。

根据图6，写出系统的闭环传递函数：（18）式中：为输出电压的拉氏变换；

Vref为输入给定的拉氏变换。

PI环的形式为：M′(s)=Kp＋（19）

式中：Kp为比例系数；

KI为积分系数。 根据劳斯判据，结合系统的超调要求，稳定裕度和调节时间，选取：

Kp=5；KI=6；K=1

5仿真波形分析

PI调节器的参数同上。首先考虑负载恒定，取Vref=28.5V，R=0.1Ω，得到输出电压的仿真波形如图7所示。由图7可见，系统在该负载的条件下，上升时间不足5s，且无超调，具有极好的稳定性。

对于负载变化的情况，采用MATLAB仿真，得到本模型在负载变化时的输出波形，如图8所示。系统带阻性负载，图8表示的负载变化情况为：在t=0时，负载电流为237A,功率为6.77kW；在t=20s时，负载突变至285A，功率为8.1225kW。

从仿真的结果看，在负载突增或突减的情况下，基于状态空间平均法的小信号模型的响应在3～4s内可以达到稳定状态，速度快，且无超调。仿真证明本模型具有良好的稳定性，在大功率大电流的情况下，能够广泛应用。

6结语

本文利用状态平均方程的小信号建模方法分析了移相全桥ZVSPWMDC/DC变换主电路的模型，着重分析了利用平均状态方程小信号建模方法的建模过程，并得出了移相全桥ZVSPWMDC/DC变换主电路的小信号数学模型。相对于其它常用的小信号等效电路法，本方法的结果可以直接计算得到，省略了对原电路的小信号处理。相对于不定负载DC/DC建模，本方法的数学表达式虽然精度低一些，但相对简单得多，因而在一般情况下更具实用价值。本方法方程列写方便，数学处理简单且直接从数学分析入手，所用推导都建立在数学理论基础上，易于掌握。通过理论研究和仿真，分析了模型的部分性能，证明本方法和结论可以广泛应用。