自适应滤波算法的仿真及工程实现
2 仿真及工程实现
2.1 LMS算法的仿真实现
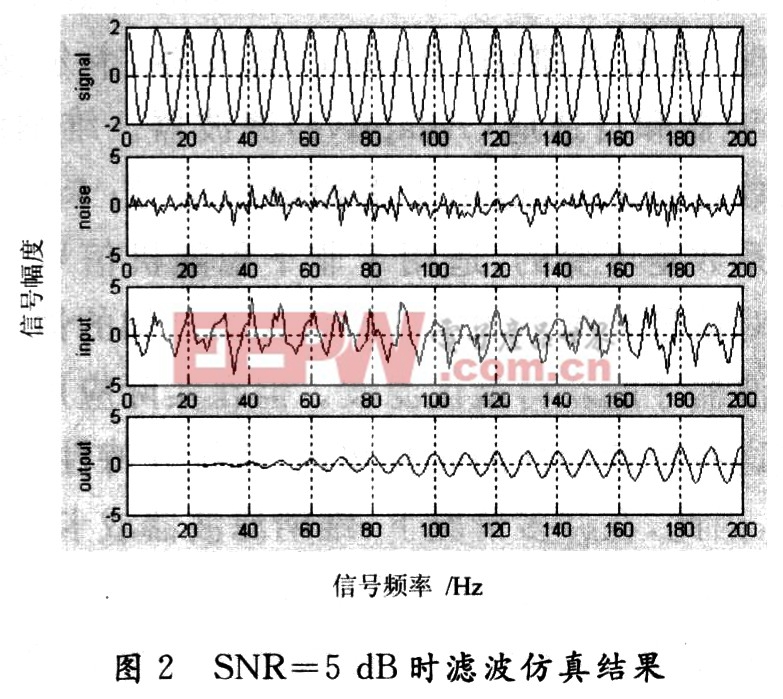
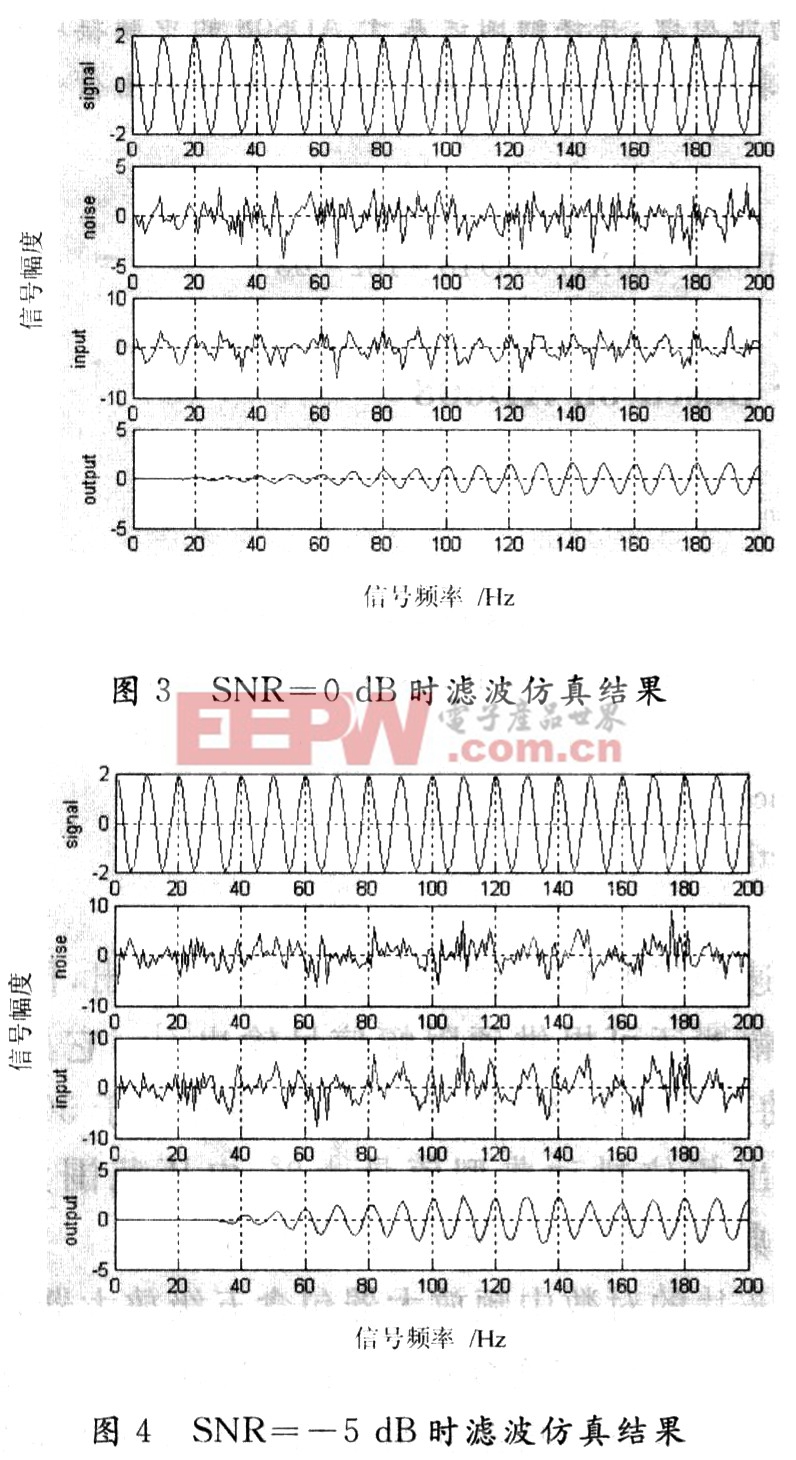
假定输入信号由正弦波信号和高斯白噪声组成。其中正弦波信号的频率f0=1 000 Hz,幅度A=2,FIR滤波器的阶数N为128;当白噪声的均值为0,其方差δ分别为0.64,2,6.32,即信噪比(SNR)分别为5 dB,0 dB,-5 dB时,采用LMS算法进行滤波的结果分别如图2~图4所示。本文引用地址:https://www.eepw.com.cn/article/173562.htm
2.2 LMS算法的DSP实现
设定采样数据的点数为1 024点,滤波器的全系数设定为128阶,自适应步长为5×10-5。设定输入信号为正弦波+噪声信号,其中正弦波的周期T=256 s,幅度A=200,正弦波信号功率Ps=20 000;噪声设定为零均值,方差δ分别为2 000,6 330,20 000,相应的信噪比 SNR=10 dB,5 dB,0 dB,根据自适应迭代公式(8),使用DSP编程实现自适应滤波算法,由DSP的CCS开发环境图形分析工具得到测试结果如图5~图7所示。
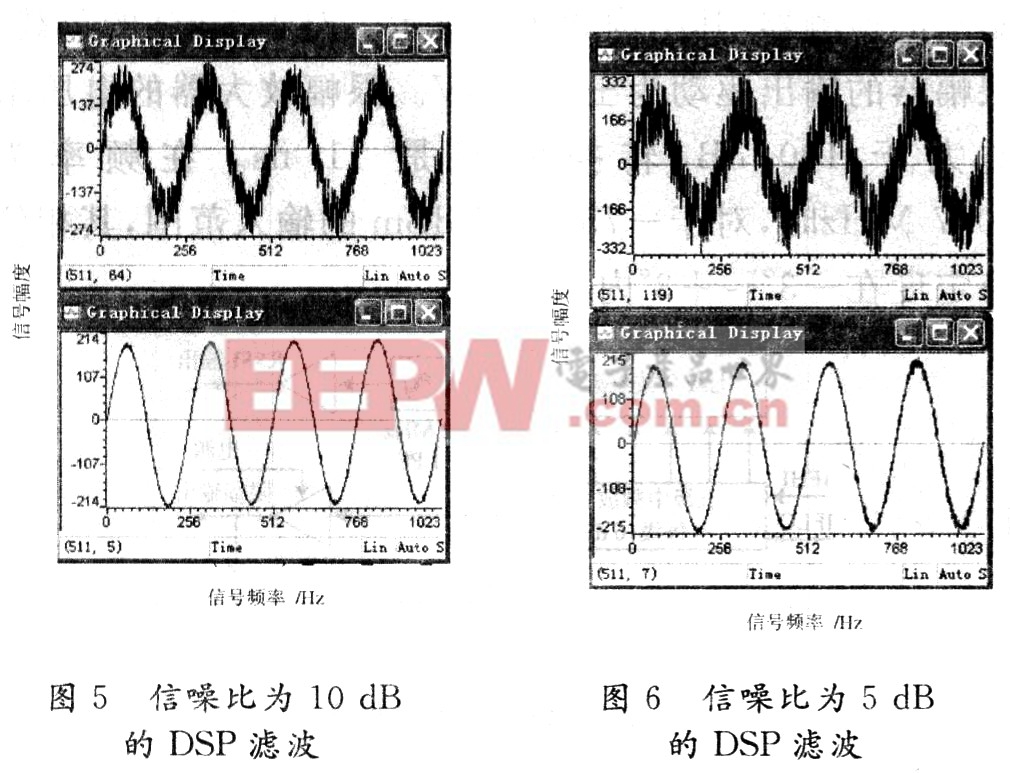
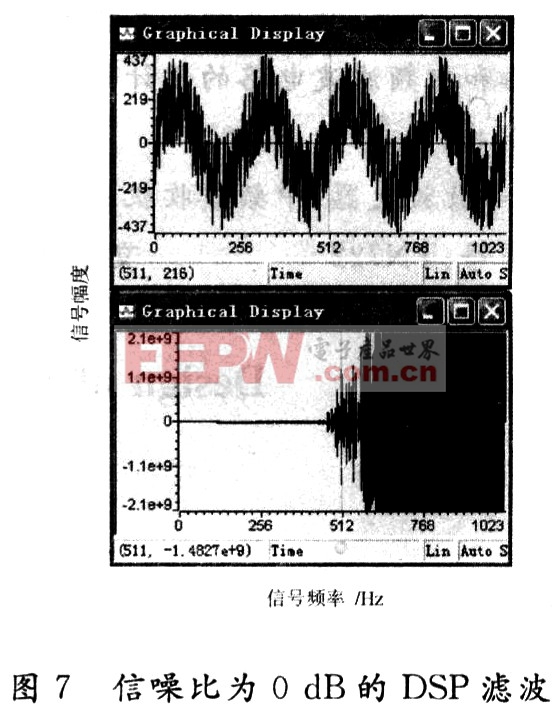
根据图7比较分析可以得出:
(1)无论是使用Matlab仿真方法还是使用DSP方法实现LMS算法,随着信噪比的降低,自适应滤波效果减弱。
(2)在信噪比位于0 dB之上时,两种方法都可以取得较好的滤波效果。
(3)在信噪比位于0 dB(或0 dB以下),仿真方法可以取得较好的滤波效果,但工程上却不能实现,即当信噪比位于0 dB时,LMS算法已失去工程上的应用价值。
3 结 语
这里在对自适应滤波理论研究的基础上,对LMS自适应滤波算法进行了研究,给出了不同信噪比条件下,LMS算法的仿真实现及基于DSP的工程实现,并对两种实现结果进行了分析比较,通过如图7所示,LMS算法在信噪比较高时,除噪效果非常显著,当信噪比较低的时候,仿真上可以得到的比较理想的滤波效果,工程上却无法实现。该结论对于指导自适应滤波理论的工程实践具有指导作用。






评论