Hopfield网络求解TSP两种改进算法的仿真研究
首先检查式(1)的前3项,其中,第3项仅在网络输出全为0时起约束作用,否则前2项已保证第3项成立。对前2项作如下修改:
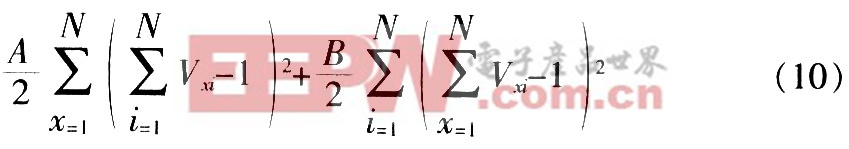
则第3项完全可省去。将优化目标项写成:本文引用地址:https://www.eepw.com.cn/article/163388.htm
或
也可满足优化要求。则TSP的能量函数简化为:

下面以式(13)作为研究对象,其对应的网络连接矩阵和外部输入分别是:

该算法可从理论上证明其有效性,仿真研究如下:取A=B=3,D=1,步长δt=0.05,对Uo=0.02和软限幅两种情况进行仿真,仿真终止条件与改进算法2相同。测试的统计结果如表2和图2所示。
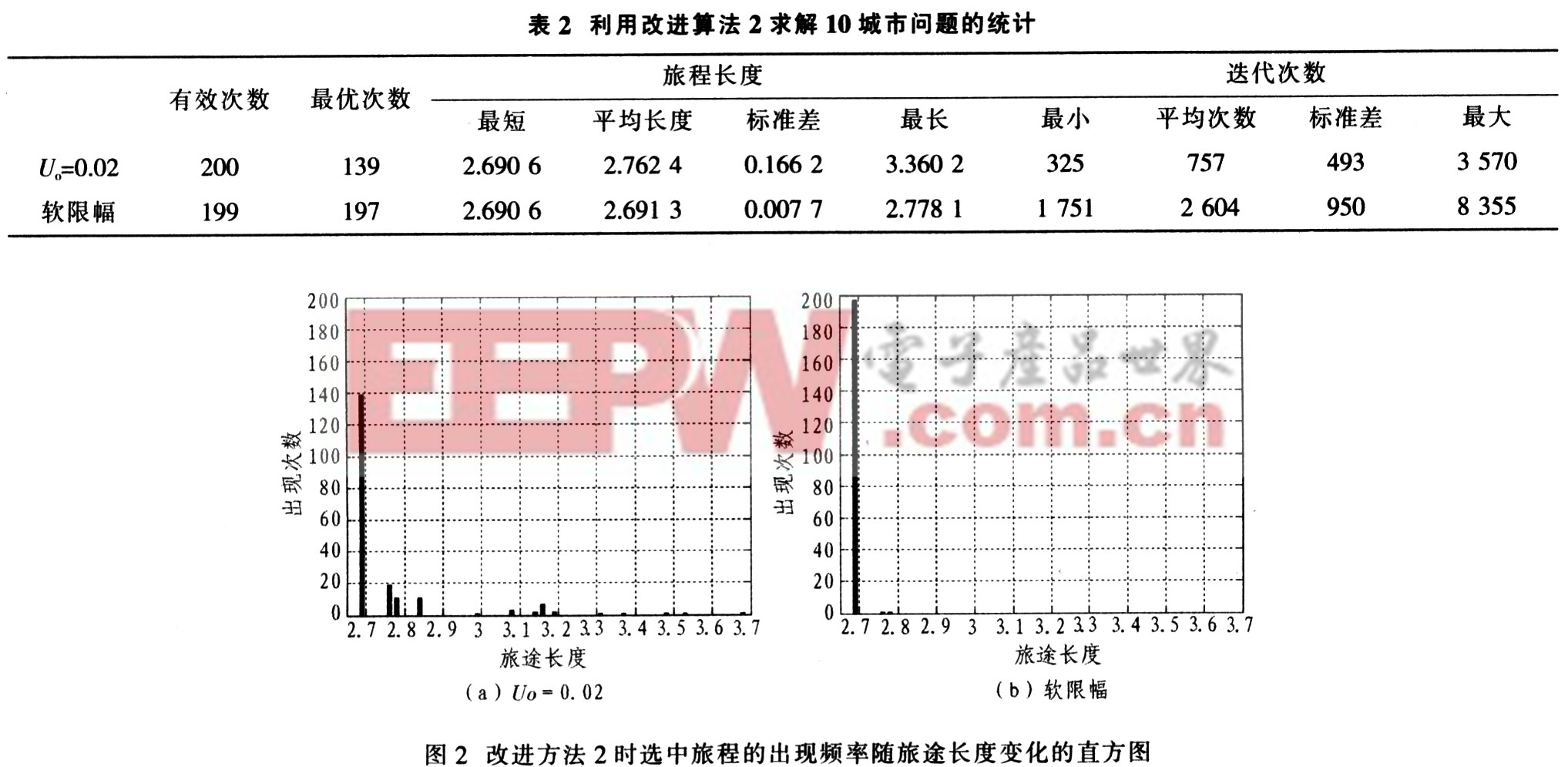
从测试结果可以看出,该方法获得的最优解的个数明显的多于改进算法1。软限幅的效果明显优于sigmold函数的效果。但所需的收敛次数较多。这一点与改进算法1是一致的。在使用软限幅时获得最优解的概率大于95%,只是所需迭代次数稍多。
4 结束语
对两种求解TSP的改进算法进行仿真研究,结果表明他们具有非常好的优化效果,在10城市问题上可近似100%的获得最优解。
另外,该算法还具有对参数敏感度低的优点。改进算法的缺点是所需迭代次数较多。当采用大步长迭代时,可降低收敛所需的迭代次数,但会影响优化效果。
这种影响对Uo=0.02的情况不明显,例如,在δt=0.5时,其优化效果与δt=0.05时几乎相同,所需迭代次数可降到450次左右。而对于软限幅的情况,步长的影响就明显了,δt= 0.5时,优化效果与图中Uo=0.02的情况差不多。下一步的工作拟采用变步长的方法,估计可大大降低所需的迭代次数。






评论