WSN中免测距距离估计算法的实现与比较
1.3 Euclidean算法
如果网络的拓扑结构不规则,DV-Hop算法的测距误差会较大。针对这些问题,Niculescu和Nath提出了另一种方法,即为Euclidean。该方法依靠锚节点周围节点的几何关系进行计算,若一个节点的两个邻居节点已知各自到锚节点的距离等于彼此之间的距离,这时,即可计算该节点到锚节点的距离了。
如图4是一个Euclidean算法的模型。本文引用地址:https://www.eepw.com.cn/article/160117.htm
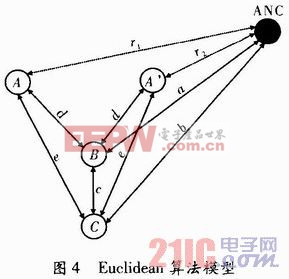
在图4中,A有两个邻节点B、C,已知B、C与锚节点ANC的距离分别是a和b,结合已知的节点间距c、d、e,Euclidean算法得到两个解:r1和r2。为确定哪个解为正解,可采用邻居节点投票的方法:若存在第3个邻居节点D,与B或C相连,且已知它到锚节点的距离。这时,可用D替换C或B,再重新计算A的位置,得到另一对解,正解必然在这两对解中,如此,用简单的选择法便可得到正解。当然,若是有更多的邻居节点参与计算,最终结果会更精确。
2 仿真实现与结果分析
默认环境如下:在100个单位的正方形场景中,有300个节点,通信距离设为15,锚节点比例设为5%,通信误差是通信距离的10%,以下从不同参数进行仿真比较。
图5是不同通信误差下,DV-Hop、Sum-Dist、Euclidean算法执行距离估计得到的标准方差,图6和图7则分别是在不同的通信距离、锚节点比例下所得到的方差。
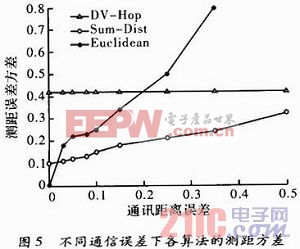
(1)Sum-Dist是3种方法中通信量最少、计算量最小的测距算法。但在通信误差10%时,其测距结果仍是理想的。实际上,有两个完全不同的趋势影响着Sum-Dist的测距精度。其一,如果完全没有通信误差,多条路径上的距离总和大于实际距离,这样就导致估计值过大;其二,由于Sum-Dist算法寻找的是最短路径,所以当存在通信误差时,其所选的路径就会比实际距离小。因为有这两个影响,通信距离的小误差反而提高了Sum-Dist的测距精度。最初,由于路径存在弯曲,导致距离估计值过大,但在最短路径的影响下,通信距离误差的增大反而使距离估计值更小。
当通信距离增大时,更多的节点可以直接通信,这样就可以得到更多的直线路径,并为最短路径提供了更多选择。所以,对于Sum-Dist算法来说,提高测距精度并不一定要增加锚节点比例。








评论