基于双混沌映射的图像加密算法研究

　　2.1 置换矩阵的构造

　　首先利用一种随机全排列生成算法来生成置换加密中所需的全排列。所谓全排列即是将M个不同元素按照一定的顺序排列起来，称为这M个不同元素的一个全排列。本置换方法分为行置换和列置换，行置换算法描述如下：

　　（1）设生成的置换矩阵大小为m×n,首先要生成一个0~M-1之间的全排列元素，元素数目为M（M>n）。

　　（2）初始化全排列矩阵，令{0,1,…，M-1}中所有元素的一个全排列为{a0,a1,…，aM-1},当i≠j时，有ai≠aj.全排列初始值系数为L,令n=?WL×M」，L可以当密钥给出，一般L在（0.5,0.7）区间即可。若太小，则产生的全排列随机性差；若太大，则数据重复多，将会增加系统的迭代次数。

　　（3）设所用混沌系统方程为xn=f（xn-1），本文用的是Logistic混沌模型，xn即为当前混沌序列，每次都要进行迭代来产生新的混沌序列。利用不等分区间的动态量化对混沌序列进行进一步处理，以增强其随机性和复杂度，本文利用判决公式（3）对Logistic混沌方程式（1）产生的序列{xn}进行判决，可以得到K=2n进

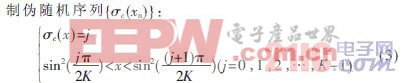
　　定义序列{xn}经过判决所在的位置构成序列为Pn={p1,p2,…，pn},其中Pi=j,即每一个xi都和一个xpi相对应，可进行两个位置元素交换，然后再重新判决，通过这样的量化即可得到n个0~M-1之间的随机数。

　　（4）初始化一个数组A,初始为空，最大长度为m,将步骤（2）生成的元素依次添加到A中，若A中不存在生成的元素，则添加到A末尾，否则舍弃。直到A中元素为n个，然后将0~M-1间元素不在A中的依次添加到A中，形成初始化全排列A.

　　（5）对初始化全排列A再进行一次全变换来增强随机性，方法同步骤（2），即将两个对应位置元素A[Pi]同A[Ppi]的交换。这里全变换的次数可以自行设定，但考虑系统运行的速度，全变换轮数r不宜过大，一般不超过5轮，由密钥给出。

　　（6）反复执行步骤（3）、（4）、（5）可得到一个m行随机全排列，即可构成m×n大小的行置换矩阵A′。

　　（7）行置换方法可看作函数B=E（A′，T），其中B为加密后矩阵，即是将T[i,j]的值赋给B[i,Ppj].列置换的方法和行置换方法相同，在此不再描述。设矩阵B经过列置换后为B′m×n.

　　该算法生成的全排列对混沌系统的初值敏感，密钥的细微差别都将产生不同的全排列。利用该算法可以生成任意多所需长度的随机全排列，算法中细微部分可以灵活处理，以增强密钥强度。

　　2.2异或矩阵的构造

　　利用Henon映射进行迭代产生随机数构成异或矩阵。由于Henon映射有一定的局限性，对常用的几种混沌模型产生的序列进行随机性测试，得出Henon混沌映射的随机性强度并不是十分理想。因此，本文用Henon混沌序列进行扰动变换后产生相关序列及参数，将输出结果进行整数取余进一步量化得到异或矩阵。其中部分细节可以灵活变换修改，在此不作详细规定。

　　（4）反复执行步骤（1）、（2）、（3），直到构成大小为m×n的异或矩阵所需随机数，设得到的异或矩阵为Cm×n.

　　（5）将异或矩阵Cm×n与所得的置换矩阵B′m×n逐一异或即可得到加密矩阵。

　　异或矩阵的使用增强了整个算法的安全性。置换矩阵和异或矩阵的使用，进一步增强了加密效果，使抗攻击能力得到增强。