基于Fuzzy c一meads的高效自适应截集算法
加入技术交流群
1 引 言
聚类在统计学、机器学习、模式识别、数据挖掘等领域得到了广泛的研究[1]。
在实际问题中，样本量可能非常大，这就无法有效地确定聚类数目，采用fcm对大样本聚类时将耗费大量的空间及时间，且有时会收敛到局部极小点上，fcm算法的缺点限制了人们对他的使用[2]。本文针对fcm算法存在的不足，在算法结构上进行了具体的改进。该方法以最大隶属度原则为指导，利用对聚类的有效性函数分析，提出了自适应截集fcm算法(s2afcm算法)，在保持模糊聚类优点的同时，提高了收敛速度，并能自适应地确定聚类中心的个数，可以避免在聚类数目的选取上存在的主观性。另一方面，在分类识别问题中，给出了正确分类和拒识的样本特征，提高了分类识别的正确性。
2 自适应截集算法
模糊聚类是无监督模式识别的一个重要分支[4]。在众多的聚类算法中，模糊c均值算法(fuzzy c-means)也是为人们熟悉的方法之一。
由于fcm算法要求聚类类别数c的先验知识，而关于数据的空间分布及结构的先验知识是很少有的，或者一点也没有，因此这一要求限制了fcm类型算法的实际应用，这就要求聚类分析中还需要研究聚类结果的有效性，以判决算法识别出的聚类是否真实。
本文所提出的自适应截集聚类方法是在xie-beni方法[5]上发展起来的，这里首先定义了聚类的紧密性：
模糊聚类的有效性函数s被定义为模糊聚类的紧密性与分离性之比，即：s-comp／sep。
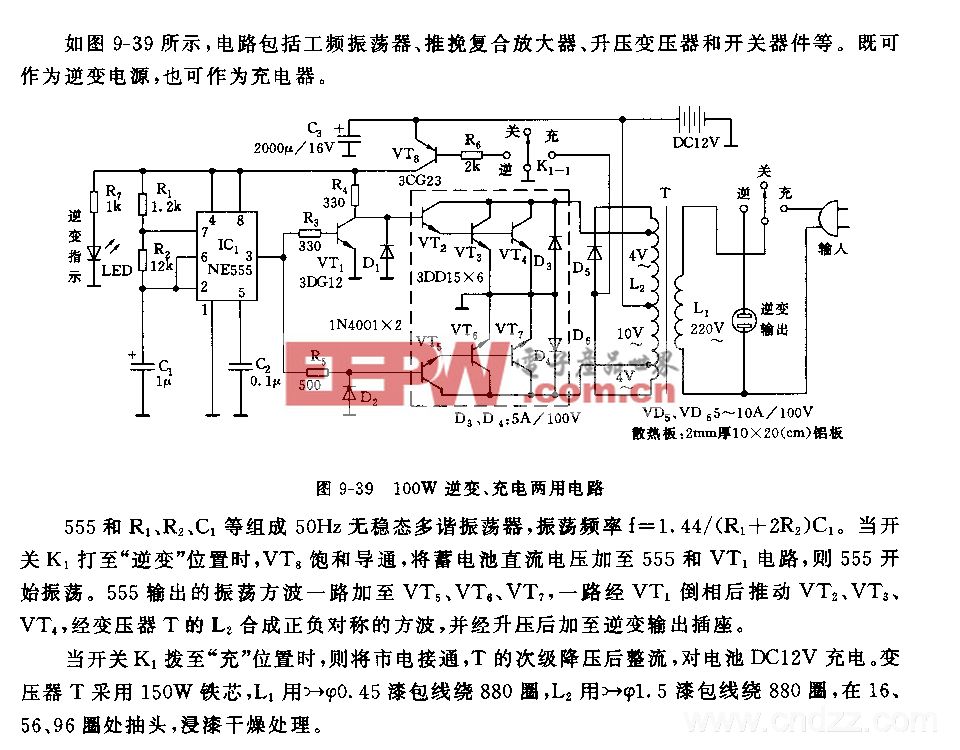
本文针对fcm算法上存在的不足，在算法结构上进行了具体的改进，增加了聚类有效性函数的分析，解决了fcm算法中初值选择问题，动态确定聚类中心的个数，可以克服主观性。
另外，使用模糊截集，在保持模糊聚类优点的同时，提高了收敛速度。
3 实验及分析使用sendmail系统调用序列进行仿真实验，主要比较2种算法的聚类效果和运行的效率。在完成了数据预处理之后[6]，依据对算法事先的假设，算法应该能够自动地对分类数c进行选择。那么实验所得到的结果应该好于模糊c均值算法。为了证明这一结论，分别用2种算法对同一数据集进行聚类并做图(图2，图3)比较，然后讨论。
以上两图分别是fcm算法和自适应截集算法对同一批数据进行聚类的效果图。在两幅效果图中，聚类中心并不在同一位置，而是有着明显差异，而且聚类中心的数目不同。产生这样的结果，其根本原因是由于算法的不同而造成的。在图2的中是硬性规定模糊c均值算法把数据集分为2类，而自适应截集fcm算法是自适应地将数据集分为4类，因而产生了上述结果。而且，通过直观的观察，比较数据与聚类中心的距离，显然，自适应截集算法的聚类结果更具有合理性，并且方便进行进一步的处理。
为了进一步比较2种算法之间的不同，在表1中用一组共有125个样本的向量进行实验给出2种算法的聚类中心和运行时间的比较。然后，再给出一个共有501个样本的数据集再做一次比较，从2个表的对比中可以看出，自适应截集算法的运行时间大于fcm算法的运行时间(单位：s)。从图1中可以得到，这是由于本算法要多次迭代寻找合适的聚类数c所消耗的时间，这种消耗换来了聚类的精确性，能够得到一个更合理的分类数。
在算法的运行效率上，s2afcm算法的时间复杂度增高了，但是当数据量增大时，如图4所示，s2afcm算法的时间增长速度却小于fcm算法。
由s2afcm得到的样本隶属度矩阵，既具有一定的明晰性，又保持了样本在空间分布的模糊性。这种划分特性对聚类以后的识别处理很有好处，一方面他减小了由模糊划分所引起的对样本进行进一步划分所需的工作量，另一方面他给出了样本空间中那些与原型的相对距离较接近的样本的模糊属性(隶属度)，以便更高层的决策机构识别或拒识，提高分类识别的正确性。
4 结 语
在实验中，可以得到一个好的聚类效果。虽然应用了模糊截集来提高收敛速度，但算法的运行效率并不能使人满意。通过算法流程图，可以看出算法消耗的时间主要是在聚类有效性的求取上，如何优化聚类有效性函数，以缩短算法运行时间是将来着重要做的工作。
评论