改进的小波阈值去噪在介质损耗角检测中的应用*
*基金项目:湖南省省市联合基金(2019JJ60060),多功能机组绝缘故障诊断关键技术研究
本文引用地址:https://www.eepw.com.cn/article/202108/427283.htm作者简介:范晋龙(1994—),男,山西,硕士研究生,主要研究方向为电气设备故障诊断。E-mail:956781676@qq.com。
黄晓峰(1974—),男,湖南,硕士生导师,副教授,主要研究方向为智能检测与控制。E-ail:7063880@qq.com。
0 引言
长期处于复杂工况下的固体绝缘材料会产生不可逆转的老化,影响电气设备的正常工作 [1]。介质损耗角可以灵敏地监测绝缘材料的老化情况,通过计算介质两端电压与泄露电流信号之间相位差得到其值。由于电流信号极其微弱,混叠了噪声的采样信号与原始信号存在较大的偏差,因此对采样信号降噪是介质损耗角检测的首要环节。小波变换由于具有多分辨率分析的特性,能够较好地区分混合信号中的有用成分和干扰成分,通过阈值设定能够对原始信号进行有选择性的剔除[2]。阈值的选择对于信号降噪效果至关重要,传统硬阈值函数降噪重构后使得信号在λ 和-λ 两处都具有不连续性;而软阈值去噪会使得信号重构后与原始信号存在很大的恒定偏差[3]。本文在对传统阈值函数进行改善后,可以克服上述两种经典阈值函数的缺陷,仿真研究表明具有较好的去噪效果,能够应用于介质损耗角的测量。
1 介质损耗角
固体绝缘材料等效电路如图1 所示,它可以看作电容和线性电阻串联的结构。
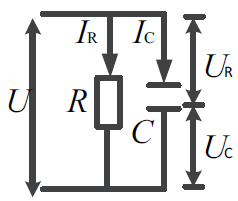
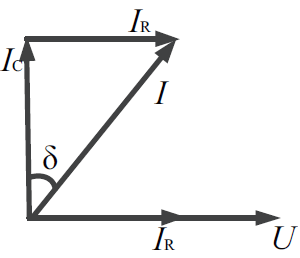
图1 串联等效电路图与向量图
理想绝缘材料电流超前电压90°,绝缘被破坏时实际电流与理想电流存在一定的相位差δ,此角定义为介质损耗角。通过电路等效模型得到的介质损耗角计算方法为:
![]()
2 小波阈值去噪
小波是一种函数,定义为式(2)。该函数可将指定复杂信号分解为不同频率分量,并对每个分量的分辨率与其尺度匹配进行研究。
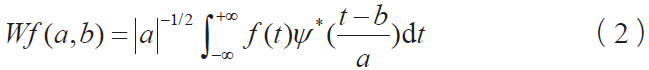
其中,ψ(t) 通过尺度伸缩和时间平移变换得到的函数系ψa,b,称为小波函数。小波函数类似于一个窗口面积固定的双窗函数,面积规律满足海森堡测不准原理[4]。小波变换的频域-时域窗口如图2 所示。
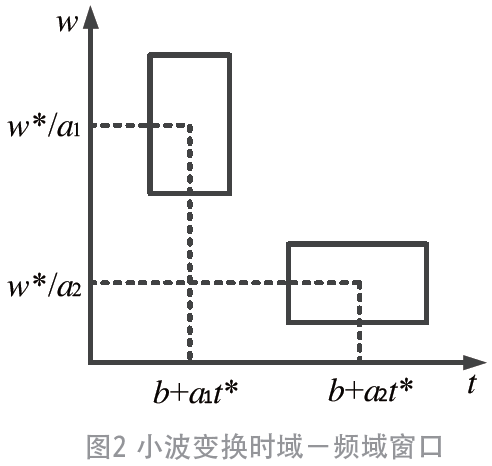
从图2 可以看出,伴随尺度的增加,时域窗会变宽,而频率窗会变窄,这是一种多分辨率的方法。当尺度较大时,适合分析混叠信号中的高频成分;尺度较小时,适合分析低频成分,因此小波变换具有混叠信号局部分析的能力[5]。
2.1 小波阈值去噪
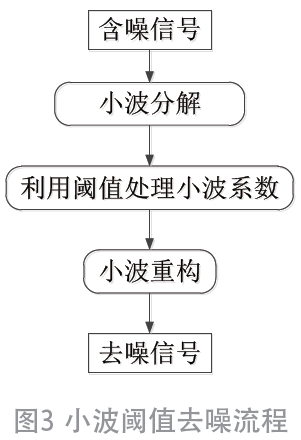
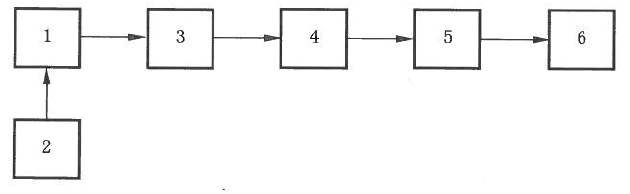
小波变换具有一种“集中”信号的能力,混叠干扰的信号通过小波变换后,重要信号的能量汇集在小波域较大的小波系数中,而噪声信号分布在整个小波域的系数中。由于重要信号和噪声信号的小波系数值存在较大的差异,小波系数较大的一般以重要信号为主,而噪声的小波系数较小。因此可以选择一个合适的阈值函数对小波系数进行选择性剔除,然后对信号进行重构,从而达到去噪的目的[6]。小波阈值去噪流程如图3 所示关键
步骤包括:
1) 小波类型、分解层数、阈值和阈值函数的选择;
2) 对含噪信号进行处理;
3) 按照阈值函数规则通过设定阈值进行干扰信号的剔除;
4) 信号重构。
2.2 改进的小波阈值去噪
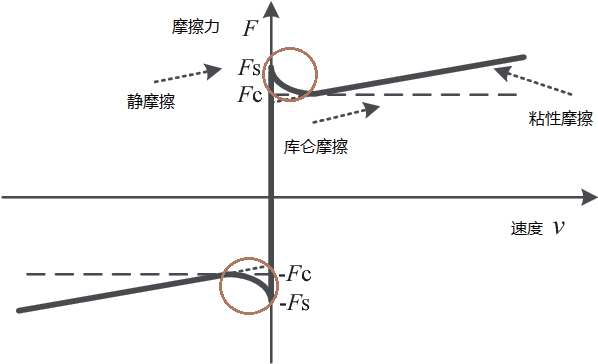
在小波阈值降噪过程中,阈值函数的选择至关重要,通常有硬阈值与软阈值函数。硬阈值函数保留了绝对值大于λ 的小波系数,可以使得原始信号的大部分信息得到保留,但在λ 与-λ 两个地方存在截断,使得重构后的信号出现不连续震荡。而相对于硬阈值函数,软阈值函数具备了在λ 与-λ 两处的连续性,但会使小波系数出现恒定偏差,从而使得重构信号和原始信号存在一定的偏差。为了解决软、硬阈值函数固有的缺陷,本文采用一种新的阈值函数:
的信号出现不连续震荡。而相对于硬阈值函数,软阈值函数具备了在λ 与-λ 两处的连续性,但会使小波系数出现恒定偏差,从而使得重构信号和原始信号存在一定的偏差。为了解决软、硬阈值函数固有的缺陷,本文采用一种新的阈值函数:
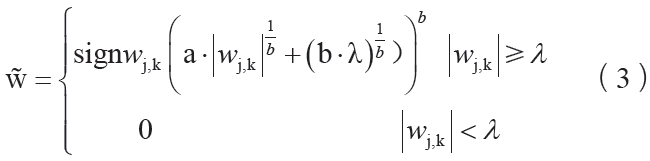
在改进的阈值函数中引进了调整系数a。当a=0 时,上式为硬阈值函数;a=1 时,上式为软阈值函数,结合了硬阈值函数与软阈值函数的优点,同时增加了调节因子b。对改进的阈值函数在λ 处进行极限计算得到:
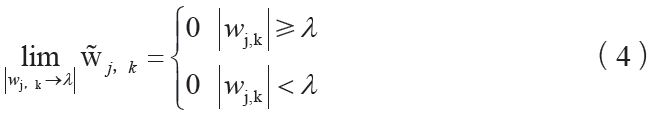
可以得到改进的阈值函数
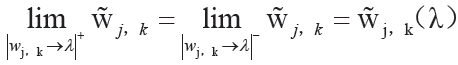
因此改进后的阈值函数具有一定的连续性,克服了传统硬阈值函数的缺点。同时,改进的阈值函数通过调节因子b 改善了小波系数的收缩程度,可以解决软阈值函数中出现的恒定偏差。
3 MATLAB仿真结果分析
利用MATLAB 实验平台产生介质损耗角的电流模型来验证本文算法的有效性,同时对原始信号叠加不同程度的噪声进行仿真研究。小波阈值去噪参数分别为:采用Sym7 小波进行5 层分解, 阈值选用固定阈值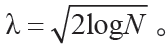 MATLAB仿真结果如图 4 所示。
MATLAB仿真结果如图 4 所示。
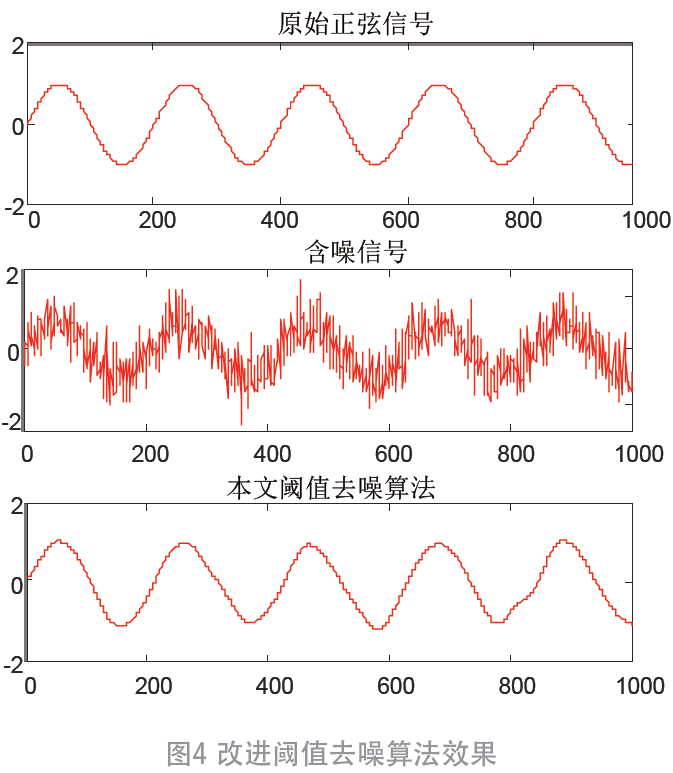
通过仿真得到降噪后信号与原始正弦信号对比结果,如图4 和表1、表2 所示。图中干扰强度为30 dB,可以看出重构信号失真度较小。同时对不同的小波阈值去噪算法效果进行对比,结果如图5 所示。在不同噪声强度干扰下,本文改进的阈值去噪算法处理后的去噪效果优于传统阈值去噪算法。
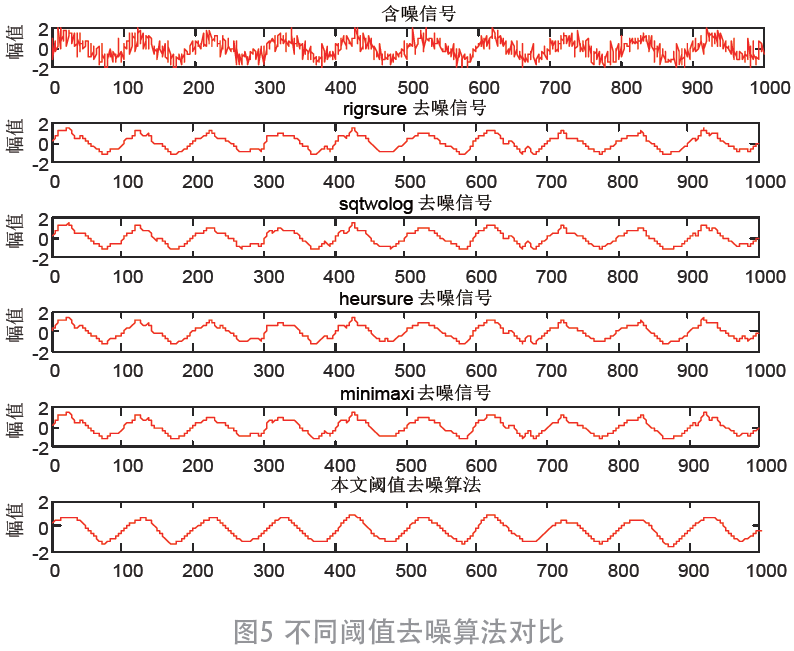
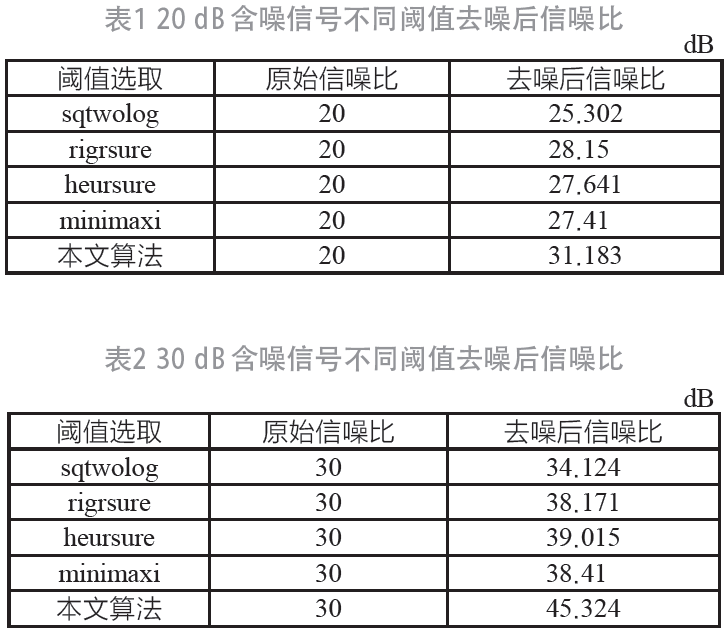
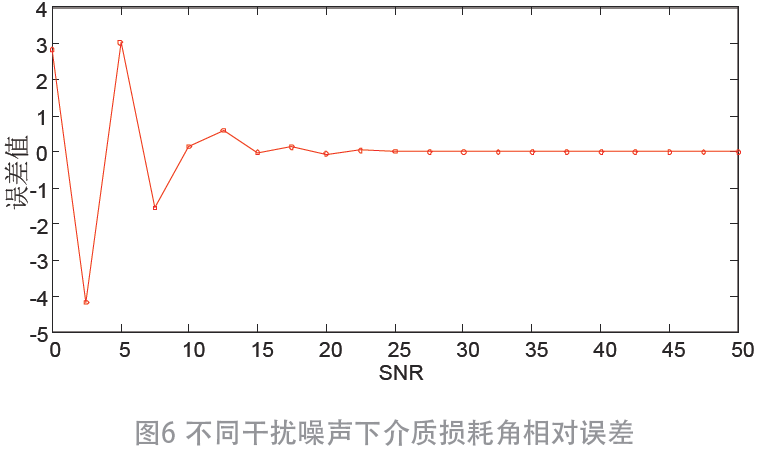
利用本文算法进行介质损耗角中相位角的计算,得到图6 所示结果,可以看出相位角计算结果在15 dB 以上噪声时,计算结果误差小,相对误差为10-5,本文采用的算法介质损耗角测量精度较高。
4 结束语
本文对介质损耗角测量过程中噪声信号的剔除展开研究,利用小波变换多分辨率分析的特点,采用小波阈值去噪对噪声信号进行剔除。由于传统的软、硬阈值函数均具有局限性,本文采用一种改进的阈值函数进行信号降噪预处理后进行介质损耗角的计算。MATLAB 平台仿真研究表明,改进阈值函数可以剔除高频噪声,重构信号失真度低,达到较好的降噪效果,有利于提高介质损耗角的测量精度。
参考文献:
[1] GAO Z,CECATI C,DING S X.A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches[J].IEEE Transactions on Industrial Electronics,2015, 62(6):3757-3767.
[2] 洪民江.基于小波变换的语音信号去噪算法研究[D].南京:南京邮电大学,2018.
[3] 谭莲子,张莉萍,解大,等.改进小波阈值去噪法在谐波检测中的应用[J].电测与仪表,2019,56(13):23-26+75.
[4] 牛艺桥,任国臣,张超,等.改进的小波阈值去噪法在电能质量检测中的应用[J].辽宁工业大学学报(自然科学版),2015,35(04):220-224.
[5] JAIN P K, TIWARI A K. A Robust Algorithm for Segmentation of Phonocardiography Signal Using Tunable Quality Wavelet Transform[J].Journal of Medical and Biological Engineering, 2018, 38(3):396-410.
[6] 洪民江.基于小波变换的语音信号去噪算法研究[D].南京:南京邮电大学,2018.
(本文来源于《电子产品世界》杂志2021年5月期)




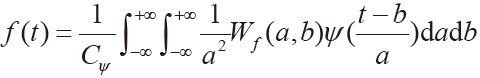




评论