对于PMSM实现全速范围无传感器控制技术的混合控制策略研究

　　王 卫，阳鹏飞，陈 瀚

　　(湖南工业大学 电气与信息工程学院，湖南 株洲 412008)

　　摘 要：对于在永磁同步电机（PMSM）中无传感器控制技术调速范围具有局限性，提出了一种结合滑膜观测器法和高频电压信号注入法的控制策略，实现永磁同步电机（PMSM）在无传感器控制技术下的全速范围控制。当PMSM处于中、高速范围内时，采用滑膜观测器法来估算转子速度和位置；在零、低范围内时，采用高频信号注入法弥补滑膜观测法的不足；当低速与中高速进行切换时，采用线性加权平均法实现平稳过度。仿真结果表明：结合滑膜观测器法和高频注入法的混合模式能够有效降低两种算法进行切换时的抖动，能够很好的实现永磁同步电机在全速范围内的平滑控制。

　　关键词：永磁同步电机；无传感器控制技术；高频电压信号注入法；滑膜观测法；线性加权平均法

　　0 引言

　　永磁同步电动机作为工业驱动领域的重要基础部件，具有可靠性高，体积小，效率高，节能，转矩相对低的优点。 随着电机控制技术的不断更新和传感器技术的快速发展，要求PMSM的性能也需要更加稳定可靠。 然而，控制方法是提高永磁同步电动机性能的关键因素 ^[1] 。 因此，研究永磁同步电动机的控制方法具有重要的现实意义。

　　永磁同步电动机的无传感器控制策略是基于永磁同步电动机的基本模型对定子绕组的电压和电流进行采样，以实现转子位置和转速的估算，但这些方法只在一定的转速范围内适用，对于在全范围内的无传感器控制却研究甚少 ^[2] 。

　　针对上述存在的问题，提出了一种基于全程调速的永磁同步电机无传感器控制策略。当PMSM以中速和高速运行时，滑动观察器用于跟踪和估计转子的位置和速度。当PMSM以低速运行时，使用高频信号注入方法来检测转子的位置和转速。 通过高频信号注入方法检测到的转子实际位置与理论预测位置非常接近，这对于提高系统的整体响应具有重要意义。

　　1 滑膜观测法在永磁同步电机中的应用

　　1.1 数学模型建立的前提条件

　　永磁同步电动机在启动过程中会出现电磁感应现象。首先建立永磁同步电动机是数学模型，先设PMSM需满足以下条件：

　　1）气隙磁场呈正弦分布，忽略谐波，三相绕组的空间相位为120°角；

　　2）忽略温度和频率变化对绕组影响；

　　3）电机中的磁芯饱和磁滞损耗的影响忽略不计。

　　1.2 滑膜观测器的数学模型

　　PMSM在d、q静止坐标系下的数学模型为：

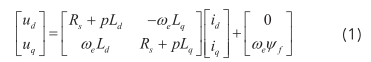
　　式中， u _d 、 u _q 分别为d、q轴上的电压； i _d 、 i _q 分别为d、q轴上的电流； L _d 、 L _q 分别为d、q轴上的电感；R _s 为定子电阻；ω _e 为转子的电角速度；ψ _f 为永磁磁链。

　　将式（1）经过PARK逆变换，可得数学模型为：

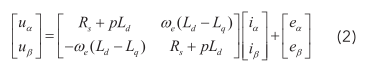
　　其中，电机反电动式模型为：

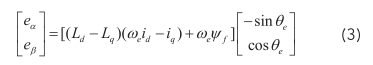
　　式中，u _α 、u _β 分别为电压在 α 、 β 轴的电压；i _α 、i _β 分别为电流在 α 、 β 轴的电流； e _α 、 e _β 分别为 α 、β 轴反电动势； θ _e 为转子的电角度。

　　则滑膜观测器方程为：

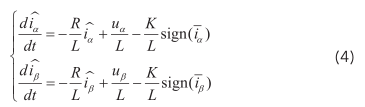
　　式中， i _α 、 i_β —电流观测值； i _α 、 i _β—电流观测误差；K—滑膜系数；sign (x)可表示为：

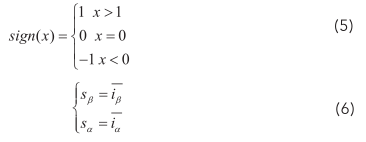
　　定义滑膜切面为s _α ，当采用函数切换控制的滑膜变结构，则

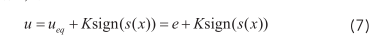
　　当系统转换到滑膜状态时，则有 s(x)=0，d/dt*s(x)=0。经过有限的时间间隔， i _α = 0 ， i _β= 0 ，令d/dt*i α(x)=0，d/dt* i β=0可得：

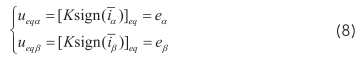
　　可得到转子位置和转速的估算值为 ^[3-5] ：

　　2 高频电压信号注入法在永磁同步电机中的应用

　　2.1 高频电压信号注入法原理

　　高频电压信号控制系统 ^[6] 如图1所示。在图中，BPF是一个带通滤波器（允许波在特定频段通过）。系统的供电方式是通过PWM电压源逆变器，这样就不会重新调整系统的结构。高频电压信号直接注入PMSM的基波激励，然后电机产生高频电流信号，锁相环方法用于处理产生的高频信号得到位置转子的信息 ^[7] 。

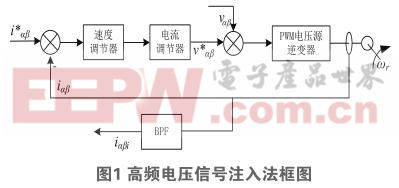
　　其中， α_β 坐标系中， v _αβ 代表电压矢量； i _αβ 代表电流矢量；上标*代表给定量； ω _r ω _r 表转子旋转角速度； θ代表转子位置角 ^[8] 。

　　2.2 永磁同步电机高频数学模型

　　当注入高频信号时，忽略PMSM的定子电阻和旋转电压和感应电动势的影响 ^[9] 。则定子电压方程为：

　　高频信号注入下的凸极PMSM的电压方程为：

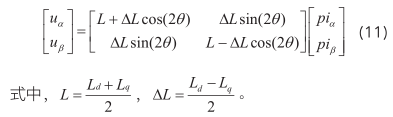
　　当注入三相高频正弦电压信号后，PMSM内产生的空间电压矢量在 α 、 β 坐标系下产生的电压方程：

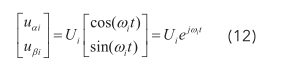
　　U _i 为幅值； ω _i 为角频率，并且ω_i≥ω_r高频的响应电流方程，可表示为：

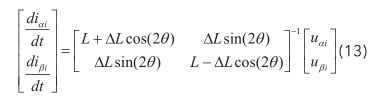
　　通过外差法得到转子信息的误差信号：

　　3 混合策略在永磁同步电机中的应用

　　3.1 基于低速到中高速控制系统设计

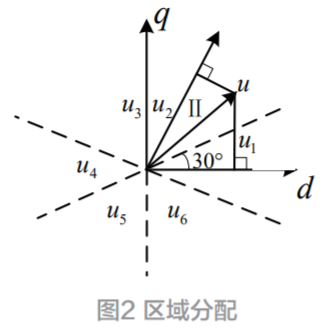
　　基于低速到中高速控制系统设计框图如图2所示，在低速状态下采用高频电压注入法，中、高速状态下采用滑膜观测器法对转速和位置的准确估算。最后将以上两种方法混合处理，采取结合各自优势的复合控制方法是实现永磁同步电机全范围无传感度控制的有效途径 ^[10-11] 。

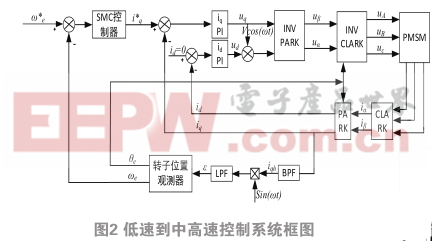
　　其中SMC控制器是用来控制电机的启动，加速模式下，闭环反馈系统中使电机以恒定的速率保持加速。使电机从低速平稳过渡到中、高速。

　　针对这种情况，当采用混合模式时：电机运行在20%的额定转速以下，切入高频电压注入法；在20%-40%的额定转速之间，通过混合算法对高频电压注入法和滑膜观测器法获得转子的位置和转速估算值进行线性比例均值处理 ^[12] ；在40%的额定转速以上，切掉高频电压注入法，只采用滑膜观测器法进行估算；则转子位置角可表示为：

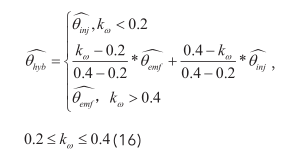
　　k _ω 为瞬时速度对额定速度的百分比，当速度达到40%时，采用滑膜观测法独立运行。

　　4 仿真验证

　　在SIMULINK中搭建仿真模型，把混合策略控制与滑膜观测法、高频电压信号注入法分别做对比，验证混合策略的优越性,PMSM参数如表1所示。

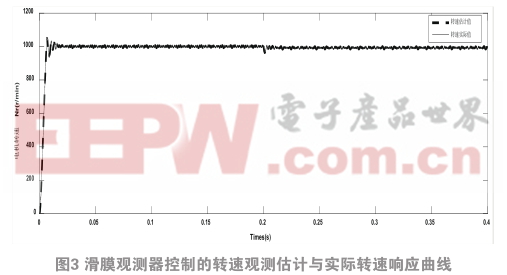
　　图3为基于滑膜观测器控制的转速观测估计与实际转速响应曲线，从图中可以看出，系统控制策略的转速期望值为1000 r/min，在开始启动时，转速最大为1050 r/min，超调为5%，回归稳态的时间大致为0.025 s时。在0.2 s时加上1 N.m的负载，在0.21 s处重新达到稳态。

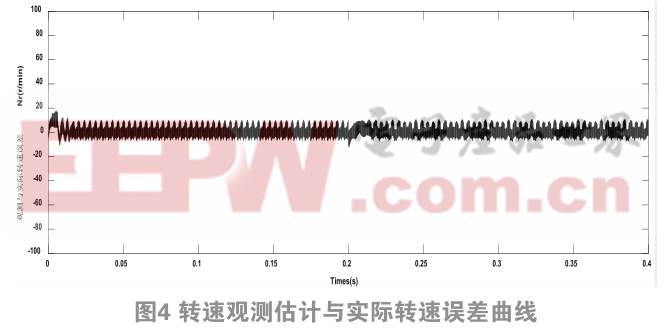
　　该种方法的转速观测估计曲线与实际转速曲线差值如图4，从图中可以看出，在开始启动时，其差值在0.01 s处达到最大为18 转。在大约0.2 s加入负载突变是位于0.21 s时差值较大，为大约为20 转，恢复时间使用大约为0.085 s。

　　从图5中可知该种方法的位置观测估计曲线与实际转速曲线，可以看出位置的估计值和实际值的误差趋近于零。

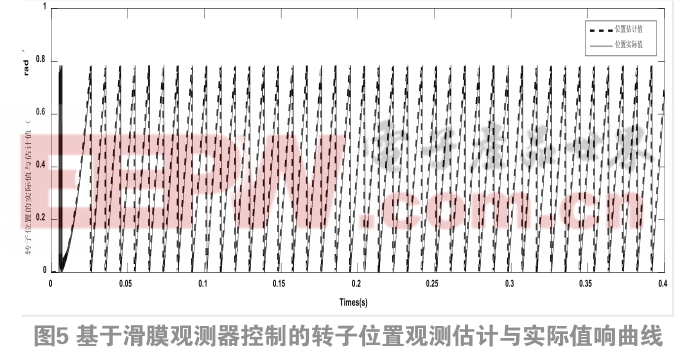
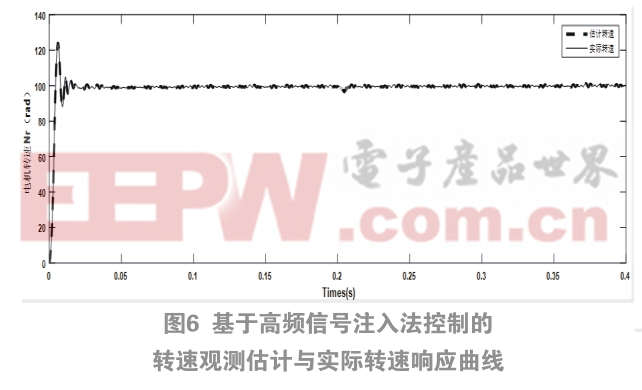
　　图6为基于高频信号注入法控制的转速观测估计与实际转速响应曲线，从图中可以看出，在开始启动时，转速最大为125 r/min，超调为25%，回归稳态的时间大致为0.025 s时。在0.2 s时加上1 N·m的负载，在0.21s处重新达到稳态。

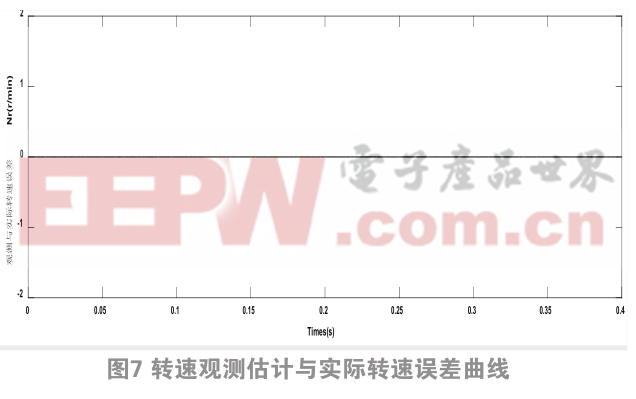
　　这种方法的转速观测估计曲线与实际转速曲线差值如图7，可以看出转速的估计值和实际值的误差趋近于零。

　　从图8可知高频信号注入法所观测的转子位置估计值与实际值误差较小，最大时约为0.096 rad。

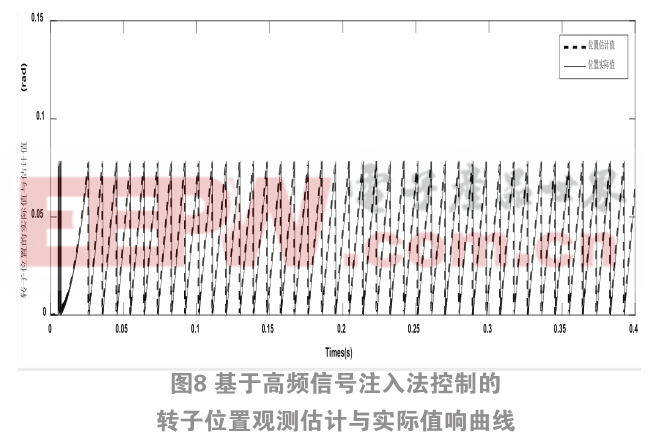
　　图9为混合控制策略下的转速观测估计与实际转速响应曲线，刚启动时，初始速度为100 r/min，0.13 s后开始进入混合估算模式，能够由低速平滑进入中高速区域。0.17 s后，电机能够稳定运行在1 000 r/min.运行到0.29 s后转速开始下降，在0.2 s时加上1 N·m的负载，在0.22 s处重新达平稳。整个仿真涵盖了低速到中速，高速到中速的运行状态过程，仿真结果可以验证PMSM全程无传感器控制在混合控制策略下的效果。 可以看出，估计的转子位置与在混合策略下观察到的实际值之间的误差在一定范围内很小，并且可以始终保持高精度，鲁棒性良好。

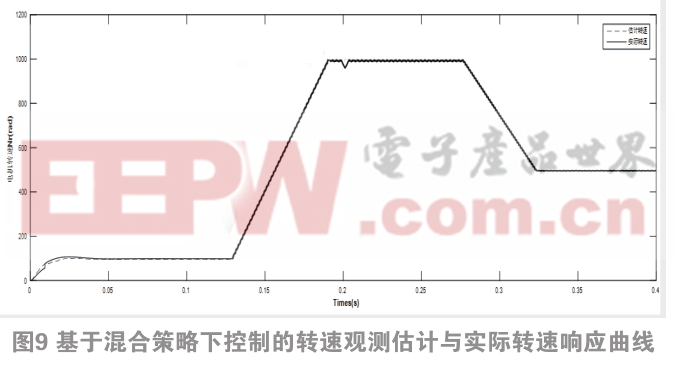
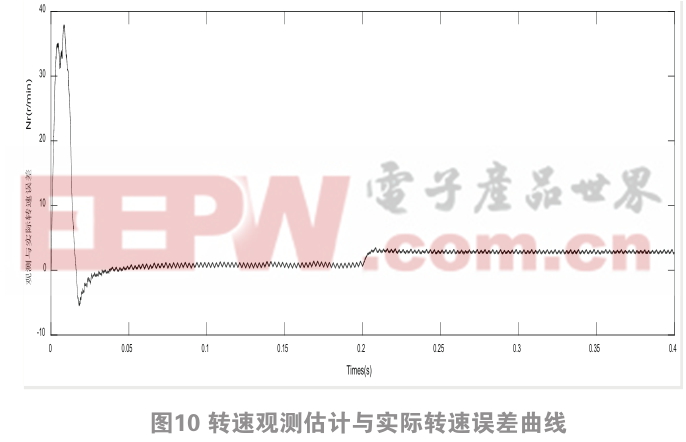
　　图10为该种方法的转速观测估计与实际转速误差曲线，可以看出在电机刚起步时，差值在0.02 s最大达到35转。到达稳定状态经过大约为0.05 s，在混合控制策略下误差较小，整个输出转速波形呈现良好的收敛效果。

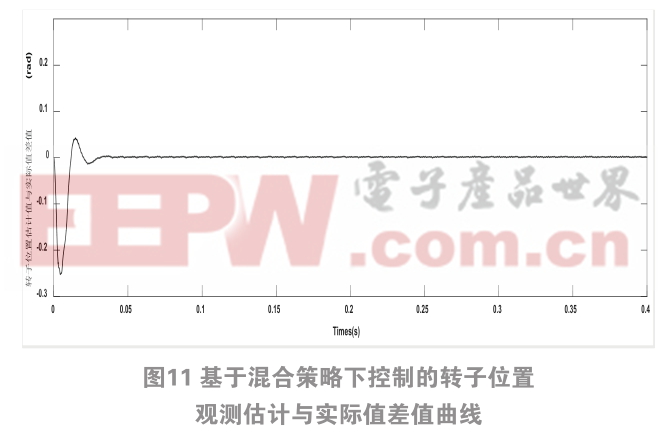
　　从图11可知此法所观测的转子位置估计值与实际值误差非常小，最大时约为0.25 rad。

　　5 结论

　　本文通过对PMSM低速到中高速全速范围运行时的不同控制方法进行研究和分析，概括了PMSM的无传感器控制系统的整体方案设计，详细介绍了高频信号注入法、滑0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4Times(s)

　　-10010203040观测与实际转速误差 Nr(r/min)

　　图10 转速观测估计与实际转速误差曲线0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4Times(s)

　　-0.3-0.2-0.100.10.2转子位置估计值与实际值差值 (rad)

　　图11 基于混合策略下控制的转子位置观测估计与实际值差值曲线膜观测法在永磁同步电机中的各自应用，分析了它们彼此的优势与缺点，提出了一种将高频信号注入法、滑膜观测法相结合的混合控制方法。仿真结果表明，将高频信号注入法和滑膜观测器法有机的结合在一起，在电机控制中能很好的对转子位置和转速进行跟踪处理，与单独使用高频信号注入法、滑膜观测法相比跟踪的速度快，并且在整个跟踪过程中，有很强的抗扰能力，鲁棒性较好，PMSM能够实现低速向高速稳定切换。

　　参考文献

　　[1] 朱军，韩利利，汪旭东．永磁同步电机无位置传感器控制现状与发展趋势[J]．微电机，2013, 46(09):11-16.

　　[2] 沈寅强，金海，戴豪宇，等．一种适用于永磁同步电机全速度运行的无位置传感器控制方法[J]．电工技术学报，2018(21): 41-43.

　　[3] 高子彦，张陈．基于MATLAB的永磁同步电机位置观测器设计与仿真[J]．电子世界期刊，2018(21): 162-164.

　　[4] Liu J, Xia P, Deng Y, et al. PMSM Speed Control Using Adaptive Sliding Mode Control Based on An Extended StateObserver[J]. High Technology Letters, 2018(04): 422-433.

　　[5] 彭思齐，宋彦彦．基于自适应模糊滑模观测器的永磁同步电机无传感器矢量控制[J]．控制与决策，2018,33(04): 644-648.

　　[6] 李浩源，张兴，杨淑英，等．基于高频信号注入的永磁同步电机无传感器控制技术综述[J]．电工技术学报，2018,33(12):2653-2664.

　　[7] 郑昌陆，胡月波．基于高频脉振电压注入的内置式永磁同步电机控制[J]．电机与控制应用，2015,37(1):10-15.

　　[8] Toh C S, Chen S-L. Design, Modeling and Control of Magnetic Bearings for a Ring-Type Flywheel Energy StorageSystem[J]. Energies, 2016, 9(12).

　　[9] 杨健，杨淑英，李浩源，等．基于旋转高频电压注入的永磁同步电机转子初始位置辨识方法[J]．电工技术学报，2018,33(15):3547-3555.

　　[10] 胡庆波，孙春媛．永磁同步电机全速范围无速度传感器控制[J]．电机与控制学报，2016,20(09):73-79.

　　[11] ALAHAKOON S, FERNANDO T, TRINH H, et al. Unknown Input Sliding Mode Functional Observers With Application toSensorless Control of Permanent Magnet Synchronous Machines[J]. Journal of the FranklinInstitute, 2013,350(1): 107-128.

　　[12] 刘计龙，肖飞，沈洋，等．永磁同步电机无位置传感器控制技术研究综述[J]．电工技术学报，2017,32(16):76-88.

　　作者简介：

　　王卫（1995-），男，湖南工业大学硕士生，主要研究方向:电力电子与电力传动。

　　本文来源于科技期刊《电子产品世界》2019年第8期第74页，欢迎您写论文时引用，并注明出处