Optistruct优化结构设计实例
本文主要介绍Optistruct软件优化方法在结构设计改进中的应用。通过使用拓扑优化和形貌优化方法对一款摩托车后挡泥板进行结构优化，使用自由形状优化方法对发动机减震衬套的截面进行优化。
一、基本知识介绍
1.优化的数学模型
优化设计的数学表达式为：
◎最小化(Minimize)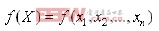
◎约束条件(Subject to)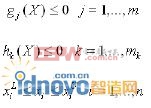
式中，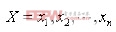
是设计变量;
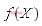是目标函数;
是不等式约束函数;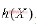
是等式约束函数。
2.Optistruct迭代算法
Optistruct采用局部逼近的方法来解优化问题。其步骤如下：
1)采用有限元分析相应物理问题;
2)收敛判据;
3)设计灵敏度分析;
4)利用灵敏度信息得到近似模型，并求解近似优化问题;
5)返回第一步。
这种方法用于每步迭代设计变量变化很小的情况，得到的结果为局部最小值。设计变量的最大变化一般发生在最初的迭代步中，此时没有必要进行太多的近似分析。
3.响应的定义方法
Optistruct中的数据卡片格式采用的是Nastran格式，因此描述响应变量的卡片主要有三种：DRESP1、DRESP2和DRESP3。其中，一般的结构响应是通过DRESP1定义;组合响应通过DRESP2或DRESP3定义，DRESP2引用卡片DEQATN定义的方程，DRESP3利用LOADLIB I/O选项标识用户定义的外部程序。对于一些多目标的优化问题，往往需要通过组合响应方法，将多目标问题转化为单目标问题。这里不做过多讨论。
4.常用的响应
主要有质量、体积、质量分数、体积分数、静态应变能、加权应变能、模态频率和Vonmises应力等。其中，质量分数和体积分数只能应用于拓扑优化分析中;在拓扑优化和自由尺寸优化中，Vonmises应力约束只能定义为全局。
二、挡泥板支架的优化
1.问题描述
图1和图2为原支架结构及断裂破坏示意图。支架发生断裂，现在采用优化的方法对结构进行改进。
2.拓扑优化
将原支架中间的孔填平，重新寻找最优的空间布局。
优化描述为：
◎优化目标：最小化单元应变能;
◎优化约束：质量分数(0.3～1.0);
◎优化变量：设计区域每个单元的单元密度。
具体步骤为：
1)先建立支架的受力工况(受力分析);
2)再建立优化工况，包括优化变量、优化约束和优化目标(该目标是建立在受力工况条件下的)。
此外，注意到结构的对称性，还需要对结果添加对称约束，如图3所示。
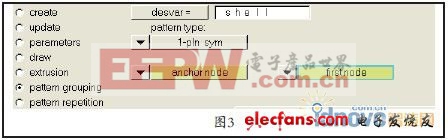
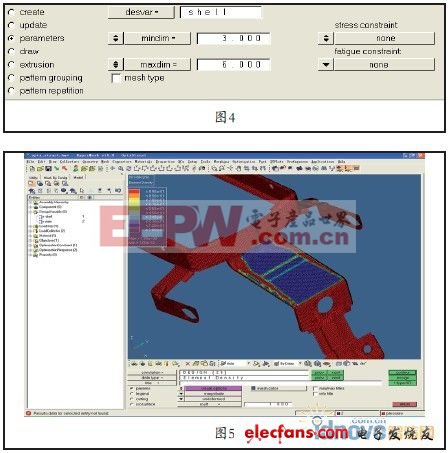
为了增加离散化和减小材料堆积，需要设置最小和最大成员尺寸，其中最小成员尺寸要大于3倍的单元平均尺寸，最大成员尺寸要大于6倍的单元平均尺寸，设置如图4所示。拓扑优化的结果，如图5所示。
3.形貌优化
形貌优化是一种形状最佳化方法，即在板形结构中寻找最优的加强肋分布的概念设计方法，用于设计薄壁结构的强化压痕，在减轻结构重量的同时能满足强度、频率等要求。与拓扑优化不同的是，形貌优化不删除材料，而是在设计区域中根据节点的扰动生成加强筋。
形貌优化的变量是通过生成内部形状变量来求解形貌优化问题，需要设置肋的最大高度和起肋角。和拓扑优化类似，它也可以设置对称约束条件。
优化描述为：
◎优化目标：最小化单元应变能;
◎优化约束：质量分数(0.3～1.0);
◎优化变量：通过节点扰动形成的形状变量。
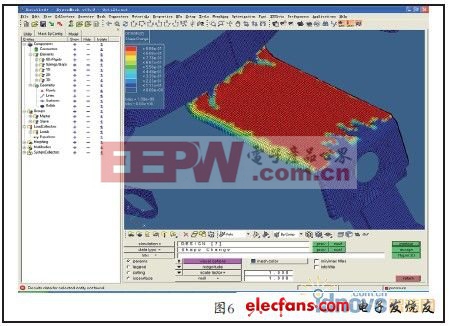
形貌优化结果如图6所示。
评论