推理控制的CVCF交流电源

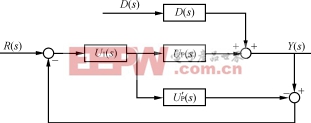
图5推理控制的CVCF系统结构图

此表所得阶梯正弦波如图4所示。这样可得到频率稳定度高的阶梯正弦波。

（2）推理控制子程序及算法

离散化推理控制的基本思想是，当系统的采样频率足够高时，采样系统的特性接近于连续变化的模拟系统，因而可以忽略采样开关和保持器，将整个系统看成是连续变化的模拟系统，从而用s域的方法校正装置D（s）。再使用s域到z域的离散化方法求得离散传递函数D（z）。设计的实质是将一个模拟调节器离散化，用数字控制器取代模拟调节器。设计的基本步骤是，根据已有的连续模型，按连续系统理论设计模拟调节器，然后按照一定的对应关系将模拟调节器离散化，得到等价的数字控制器，从而确定计算机的算法。　　首先将离散化令K1=250,

T1=0.015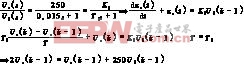再将离散化

　　得308Uk(k)=490Uk(k－1)－185Uk(k－2)

＋19Ue(k)－5Ue(k－1)

又Uk(k)=Ur－[Uf(k)－Uc(k)]

　　∴2Ua(k)=Ua(k－1)＋250Uk(k－1)(1)

Ue(k)=Ur－[Uf(k)－Ua(k)](2)

　　308Uk(k)=490Uk(k－1)－185Uk(k－2)

＋19Ue(k)－15Ue(k－1)(3)

当根据（1）、（2）、（3）可得推理控制的输出

　　令K1=2,K2=1,K3=250,K4=308,K5=490,K6=185,K7=19,K8=15

∴K1Ua(k)=K2Ua(k－1)＋250Uk(k－1)(1)

Ue(k)=Ur－[Uf(k)－Ua(k)](2)

K4Uk(k)=K5Uk(k－1)－K6Uk(k－2)

＋K7Ue(k)－K8Ue(k－1)(3)

3推理控制的CVCF抗扰性能分析

推理控制的CVCF是一个输出可测、而扰动不可测的系统，设电源的输出为Y（s），输入为R（s），扰动为D（s），此时的电源不需要二次输出和估计器，只需一个估计模型，推理控制的CVCF系统结构如图5所示。

此时的系统输出为推理控制器Gi(s)=Gf(s)/Gp(s),当Gp(s)=Gp(s)时，系统输出为

Y（s）=Gf(s)R(s)＋[1－Gf(s)]B(s)D(s)

当Gp(s)≠Gp(s）时，系统的输出为当滤波器的稳态增益为1时，在给定的阶跃扰动下，系统的主要输出Y（s）=R（s）；在阶跃扰动不可测的情况下，系统的主要输出稳态偏差为Y（0）=0。

可见，系统具有非常好的性能，不管模型有何种误差，系统的主要输出总是稳态无偏差的，而且控制系统的可调参数很少。