基于可拓控制算法的改进与仿真研究

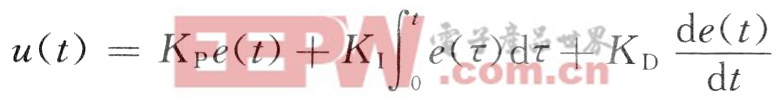
其中：e(t)，u(t)分别为PID控制器的输入和输出；KP，KI，KD三个参数的整定采用Ziegler一Nichols方法。为方便起见，此时记u(t)=u(PID)。
(2)测度模式M2。采用改进的可拓控制算法，控制器的输出为：

u(t)=y(t)／k一K(s)psgn(e)+D(s)sgn(e)
其中：u(t)，u(t一1)分别为控制器当前时刻和前一时刻的输出；y(t)为当前时刻被控量的采样值；k为过程的静态增益；Kci为第M2i个测度模式的控制系数；K(s)为特征状态S的关联度；D(s)为状态距；户为修正因数；sgn(e)为偏差的符号函数，与上述取法相同。
(3)测度模式M3测度模式M3对应的特征状态较大地偏离经典域，处于非域范围内，此时控制器的输出取幅值。
综上所述，可拓控制器的输出算法如下：

2 可拓控制算法的仿真研究
在该仿真部分，将采用相应的线性对象、延迟对象和非线性对象对改进的可拓控制算法进行仿真试验，并与传统的可拓控制算法和PID控制算法进行比较。其中，PID控制参数的选取均采用Ziegler-Nichols方法整定后的参数，输入信号为单位阶跃信号，仿真时间为500 s。
2．1 线性对象
取线性对象的传递函数为：G(s)=1／(10s+1)4，则控制效果如图3所示。

图3中，PID表示PID控制输出，EC表示传统的可拓控制算法输出，IEc表示改进后的可拓控制算法输出。
由图3中曲线可知，在误差允许范围内，PID控制、EC和IEC均能收敛，从而达到较满意的控制效果。与其他两种控制方法相比，IEC不但能更快地收敛于稳定值，而且超调量也比较小。
2．2 延迟对象
取延迟对象传递函数为：G(s)=e-10s/(5s+1)4，则控制效果如图4所示。

由4图中曲线可知，在误差允许范围内，PID控制、EC和IEC均能收敛从而达到较满意的控制效果。与PID控制相比，IEC能更快地收敛于稳定值；与EC相比，除了能更快地收敛外，IEC的波动较小、超调量几乎为0。
2．3 非线性对象
取非线性对象为开环传递函数G(s)=1／(10s+1)4的单位反馈输出的平方，控制效果如图5所示。

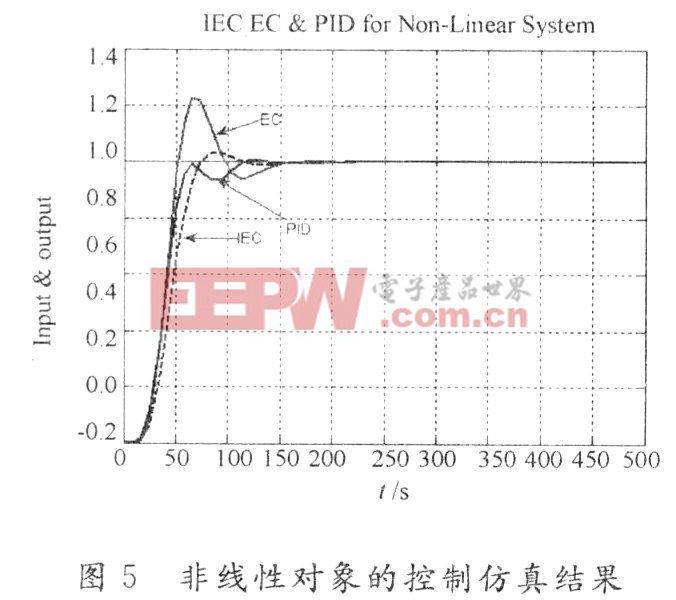
由图5中曲线可知，在误差允许范围内，PID控制、EC和IEc均能收敛从而达到较满意的控制效果。与PID控制相比，IEc能更快地收敛于稳定值；与EC相比，除了能更快的收敛外，IEc的波动和超调量均较小。

3 结 语
从仿真研究来看，改进的可拓控制算法具有参数整定简单、响应快速且稳定等特点。并应用于线性对象、延迟对象和非线性对象进行仿真研究，验证该算法的可行性和有效性。结果证明了可拓控制具有良好的控制品质和较好的自学习能力，有较好的发展前景。