振动筒式压力传感器的FLANN非线性校正
表1 传感器在温度20℃时的部分压力标定值数据
压力mmHg | 172.295 | 197.183 | 203.625 | 210.804 | 218.798 | 227.800 | 232.745 | 237.481 |
周 期 | 2000 | 1000 | 800 | 600 | 400 | 200 | 100 | 10 |
在实验过程采用较为流行的MATLAB软件进行仿真。初始化中,学习因子取值为1.1,误差e取值0.00035,n=3。经过多次迭代,不断调节网络的连接权值,最终求出权值,确定了式(1)中多项式的系数为:a0=237.6144,a1=-54.1649,a2=2.9464,a3=0.001129。所以该振动筒压力传感器的校正函数为:
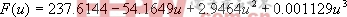 (5)
(5)
表2传感器在温度20℃时的部分压力计算值与标定值的比较
压力mmHg | 172.425 | 197.255 | 203.682 | 210.711 | 218.858 | 227.891 | 232.798 | 237.375 |
周 期 | 2000 | 1000 | 800 | 600 | 400 | 200 | 100 | 10 |
根据所得以上函数,对-40℃~60℃范围内8个温度点的标定值和由方程式(5)所得的估计值进行了比较。在表2中列出了温度在20℃时的估计值,和表1比较可知该模型的精度较高。其最大相对误差小于0.08%,完全可以满足大多数工程允许的误差,以实现压力非线性校正。
5结论
使用函数链神经网络进行振动筒式压力传感器非线性校正具有结构简单、自学习能力强、易于收敛、效果良好的特点。它的训练的确比BP算法容易,而且算法也简单得多;是一种很好的非线性校正方法,它也可以完全用于其他类型传感器的非线性校正。









评论