用神经网络控制的二象限开关电感DC/DC变换器

3．1连续模式

图4连续和非连续区的边界图

图5连续和非连续区的边界图

　　若等效电阻R很小，则电阻R上的电压降可以认为是RIL。

由此可见传输效率仅取决于导通占空比k、源电压和负载电压，与R、L和f无关。

3．2非连续模式

　　连续和非连续区的边界如图5所示。从方程（49）可以看出非连续导通区是由下列因素产生的：

　　（1）开关频率f太低；

　　（2）导通占空比k太小；

　　（3）电感L太小；

　　（4）负载电阻R太大。

　　整个导通周期远小于T。假设导通周期位于0和t4之间，电感L上的电压和电流为：

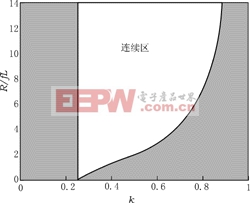
图5 连续和非连续区的边界图

iL(kT)是电感电流iL(t)的峰值，同时也是变化量ΔiL的峰—峰值。当t=t4时，由方程（52）可得iL(t4)=0。

4神经网络控制

　　这种变换器工作于开环控制方式。由公式（17）和（47）可见，因为电路的电阻R是一随机参数，所以它对系统的工作点有很大的影响。为了获得一个稳定的变换运行，我们在系统中采用神经网络控制[7,8〗。神经网络控制包括一个由比例加积分（PI）运算和神经网络组成的闭环控制。这一系统的全图如图6所示。

　　比例加积分（PI）运算在4.1中叙述。神经网络由三层组成，分别是输入层、隐含层和输出层。神经网络的结构如图7所示。三层中所有节点的函数如图8所示。它们分别在4.2和4.3中叙述。

4.1数学模型

　　比例加积分（PI）运算由一个比例加积分控制器和负载组成。式中：τ=L/R,Vi在开关接通时为Vl，在开关关断时为V2。

图6用神经网络控制的二象限开关电感DC/DC变换器

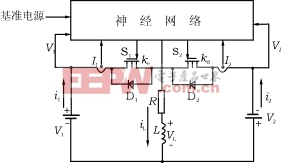
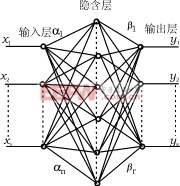
图7神经网络

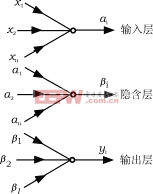
图8节点函数