基于BOTDA技术的电缆温度监测
加入技术交流群
2 电缆的分布式布里渊散射光纤传感器实验
本实验的目的有两个。1)通过光纤测温获取电缆温度变化数据；2)验证布里渊光纤温度测量设备的性能。实验电路的搭建如下所述。
将BOTDA的分布式光纤温度应变分析仪与实验电缆内的2根光纤，熔接在一起形成一个回路，进行数据采集与分析。实验时将电缆的一端，通过象鼻子将铜缆1和铜缆3连接，电缆的另一端的铜缆1和铜缆3分别接到大电流发生器的正负极。将电缆连接成回路，用于电缆加热。分布式布里渊散射光纤传感器测得的数据如图2所示。本文引用地址：https://www.eepw.com.cn/article/161061.htm
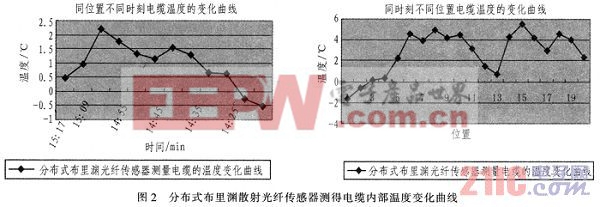
分布式布里渊散射光纤传感器能基本探测到电缆内部温度的变化和温度的分布。从同时刻不同位置电缆温度的变化曲线可以看出，温度变化先升温后下降。这种情况和实际情况是吻合的。因为电缆两端的铜缆是裸露在空气中的，铜缆的中间部分是包裹在护套和铠装中的，所以电缆的温度变化是先升温后下降，然后在升温，最后是下降。由此可以得出，分布式布里渊散射光纤传感器可以测出电缆内部温度的变化。
为了验证基于分布式布里渊散射光纤传感器测温误差小，而且能够测量出电缆温度的变化趋势和实际温度变化趋势基本吻合的。本实验采用了热电偶去测量电缆线芯温度的变化，与光纤测温作对比分析。
3 数据处理及结果分析
为了验证我们得到的温度数据的正确性以及更直观的分析出电缆温度的变化，我们对实验数据进行拟合处理。首先我们通过滤波器滤除由于忽略工作环境下实验设备测量不准确性带来的误差；然后我们将这些剔除误差的实验数据进行拟合处理；最后我们通过数据拟合的数据曲线来分析温度的变化趋势。文中用最小二乘法对处理后实验数据进行数据拟合。
最小二乘法基本原理：从整体上考虑近似函数p(x)同所给数据点(xi，yi)(i=0，1，…，m)误差ri=p(xi)-yi(i=0，1，…，m)的大小，常用的方法有以下3种：1)误差ri=p(xi)-yi(i=0，1，…，m)绝对值的最大值
，即误差向量r=(r0，r1，…，rm)T的∞-范数；2)误差绝对值的和，即误差向量r的1-范数；3)误差平方和
的算术平方根，即误差向量r的2-范数；前两种方法简单、自然，但不便于微分运算，后一种方法相当于考虑2-范数的平方，因此在曲线拟合中常采用误差平方和来度量误差ri(i=0，1，…，m)的整体大小。
数据拟合的具体作法是：对给定数据(xi，yi)(i=0，1，…，m)，在取定的函数类φ中，求p(x)=φ，使误差ri=p(xi)-yi(i=0，1，…，m)的平方和最小，即
从几何意义上讲，就是寻求与给定点(xi，yi)(i=0，1，…，m)的距离平方和为最小的曲线y=p(x)。函数P(x)称为拟合函数或最小二乘解，求拟合函数p(x)的方法称为曲线拟合的最小二乘法。
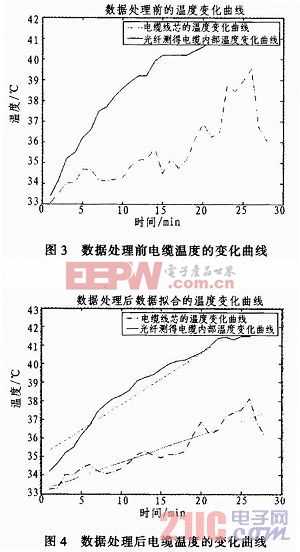
通过Matlab编程去除了数据中的误差并绘出了海缆数据处理后的温度变化曲线。如下图3和图4所示。
评论