有源滤波器中的相位关系考察

　　其中低通滤波段的相移-频率特性属于一个反相的二阶型响应(参见图4，右轴)，高通段电路将具有反相高通响应(参见图5，右轴)。

　　双二阶(biquad)

　　状 态变量滤波器的一个近亲是双二阶型(参见图15)。该电路的名称最早是由J. Tow于1968年使用的(见参考文献6)，后来由L.C. Thomas 于1971年使用(见文献5)，其工作是基于如下的事实：传递函数是两个二阶项之比。该电路与状态变量电路之间存在轻微的区别。在这一结构中，不能提供单 独的高通输出。不过它具有两路低通输出，其中一路是同相的(LOWPASS1)，另一路是反相的(LOWPASS2)。

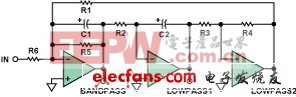
　　图15. 标准的双二阶2极点电路

　　由于添加了第四个放大器电路，故可以实现高通、陷波(低通、标准和高通)以及全通型滤波器。图16示出一个带有高通电路的双二阶电路的原理图。

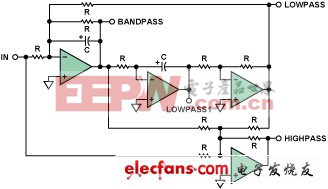
　　图16. 2极点双二阶滤波器(带有高通段)

　　其中LOWPASS1段的相移-频率特性属于同相、二阶、低通型响应(参见图4的左轴)。LOWPASS2段将具有反相的二阶型响应(参见图4，右轴)。HIGHPASS段的相移特性属于反相特性(参见图5，右轴)。结论

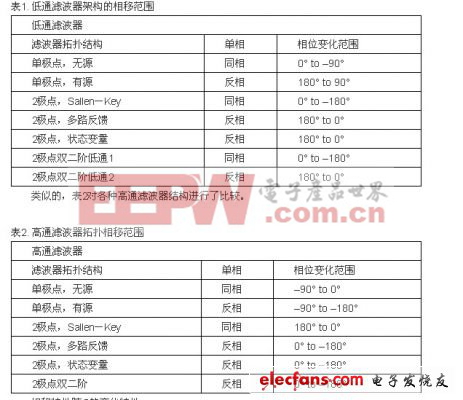
　　我们已经看到用于构建一个滤波器的拓扑将影响其实际的相位响应。这会是确定所用的拓扑时需要考虑的一个因素。表1对本文中讨论的各种低通滤波器结构的相移范围进行了比较。

　　相移特性随Q的变化特性

　　上述的2阶响应的Q值都是0.707。图17示出了Q的变化对低通滤波器的相位响应的影响(对高通滤波器的影响也 类似)。图中绘出了Q = 0.1，0.5，0.707，1，2，5，10和20时的相位响应曲线。值得注意的是，Q值较低的情况下，在远低于截止频率的频率上相位就开始发生变化。

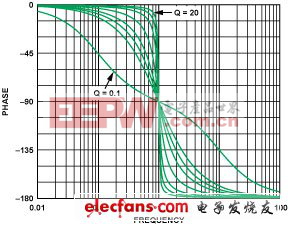
　　图17. 相移随Q值的变化特性

　　虽然幅值响应随Q值的变化并非本文的主题，但也是一个令人感兴趣的问题。图18示出了Q值在上述范围内变化时一个2阶滤波器的幅值响应特性。

　　当 高Q电路应用于多级滤波器时，高Q电路的响应特性的尖峰现象也是令人感兴趣的问题。虽然在理论上这些电路段以何种顺序来级联并无差异，而在实践中，把Q值 较低的电路段置于高Q电路段之前将更为有利，这是为了让尖峰现象不致于超出滤波器的动态范围。虽然该图是针对低通段的，但高通响应也存在类似的尖峰。

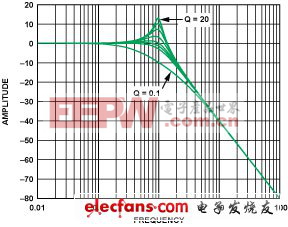
　　图18. 随着Q值的变化，2极点滤波器的幅值尖峰特性的变化