Cyber15队智能汽车竞赛技术报告(节选)

　　然后，将卡尔曼滤波矩阵形式转化为方程形式：
       
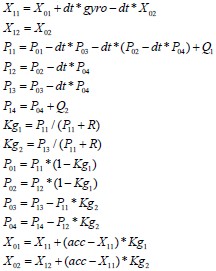
　　这里，X01即为我们需要的角度卡尔曼滤波值。

　　可以看到的是，卡尔曼滤波方程形式共有14个公式，同时很多参数的运算涉及浮点数，这对于单片机的高效运行时极为不利的，因此我们需要通过一些方法对卡尔曼滤波的公式进行化简，从而在不失精度的情况下，尽可能减小运算量。

　　需要注意的是，Q,R两个参数是关于传感器和系统的方差，他们随着系统的工作状况不同而会产生相应变化，对应到我们的系统，在车模运行状态不同(倾角不同，PWM不同)情况下，Q,R都是不同的。

　　根据相关参考文献，Q,R虽然都是关于时间的变量，但是由于卡尔曼滤波有很好的收敛性，所以可以将Q，R都取比较极端的参数。用常量来定义。然后再看图3，注意方框中的公式，根据我们的观察，不难发现，整个方框中都是为了获得卡尔曼增益(矩阵Kg)，我们设想，能否使用一个常数来等效替代卡尔曼增益那?根据我们在实验中的观察，卡尔曼增益是一个收敛的变量，并且针对到我们的这个系统，他的值非常小，直立状态下趋近于一个常数。(所有这些工作都在MATLAB下完成)

　　所以，我们将方框中的所有公式完全省略，通过实验整定，选取一个近似Kg来替代方框中的所有运算。同时，通过NATLAB观测各变量的变化趋势，我们尝试让Kg2=0(Kg1，Kg2本身就是非常小的变量，所以可以让其等于0)。并发现Kg2对于整个卡尔曼滤波的影响非常有限。所以将Kg2设定为0。

　　以下就是我们组程序中卡尔曼滤波的简化算法实现
         

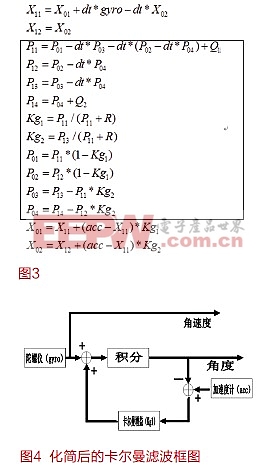
　　X1=X0+gyro*dt;
　　X0=X1+(acc-X1)*kg;
　　化简后的卡尔曼滤波框图如图4。

　　卡尔曼滤波参数整定

　　化简后的卡尔曼滤波主要是对dt以及Kg两个参数进行整定。需要特别指出的是，这里的dt并不只是一个采样间隔。由于陀螺仪的输出和加速度计输出的量纲并不相同，所以陀螺仪采样值*dt并不直接反应一个角度，而是与实际角度相差一个系数。因此此处的dt可以等效理解为dt=采样间隔*比例系数。

　　dt越大，积分速度越快，卡尔曼输出追随实际角度的情况越好(当然不能太大，不然可能会出现超前相位)。但是dt越大，陀螺仪漂移造成的影响也就越大。

　　Kg决定了加速度计的权重。Kg越大，实际输出的漂移就越小，但是滤波效果的噪声也就越大。

　　所以dt和kg是一对矛盾，不能太过于极端。

　　首先是静态整定。

　　将车模保持在稳定直立状态，让车轮以恒定PWM(80%以上)转动，然后调节参数。