用于量子计算的Sub-1K冷却:第 1 部分
需要新技术和对旧技术进行改进,以达到 <1 K 的量子计算冷却。
出于多种原因,各种形式的量子计算是当今的热门话题。它提供了解决其他棘手的数值问题、编码和解码超级密码等等的潜力。它受到了媒体的大量炒作,但更重要的是,大学、政府研究人员和拥有大量研发预算的私营公司正在向该学科投入大量资金。讨论进展的论文和宣传进展的新闻稿正在成为常态。
虽然已经取得了相当大的进展,但我们不太可能在未来五年或十年内看到便携式甚至台式量子计算机(当然,我们应该“永远不要说永远”,不可预见的突破确实会发生)。
造成这种情况的原因之一是这个热门话题需要极冷才能发挥作用。这不是液态氢在 20.28 K(-252.87 °C 或 -423.17 °F)下的低温;相反,它需要超低温的 1 K 以下区域,下降到毫开尔文 (mK) 区。
本文不是有关量子计算的教程。相反,它着眼于与该主题相关的一些背景、既定的冷却方案以及有助于实现和维持所需 <0.1 K 温度的新制冷方法。
通过这样做,我们将深入研究一个在许多方面违背常识和直觉的世界,但它存在并且非常真实。在这个“诡异”的量子计算世界中,经典物理学和电子学在某种程度上被搁置一旁。
为什么这么冷?
量子比特(称为量子比特)与传统的数字电子比特不同,后者要么处于逻辑 1 状态,要么处于逻辑 0 状态。相反,它们同时存在于所谓的两种状态的叠加中。这种违反直觉的状态使量子计算机能够同时经历大量的可能性,并可以利用这些可能性来实现量子算法。
但是,与传统处理器一样,您需要一个已知的启动状态。对于量子比特,这称为信托状态,并与最低能量状态相关联,称为逻辑状态 0。这种初始状态下的不确定性成为贯穿所有量子算法步骤的起点误差。因此,量子比特初始化得越接近其“接地”状态,信托状态出现不确定性的可能性就越低。永远记住,我们处于量子层面,所以我们在这里处理的是概率而不是确定性。
让这些量子比特达到基态的方法一点也不奇怪:冷却它们以消耗尽可能多的能量,这样就会更少的量子比特被诱导到激发的逻辑 1 状态。请注意,这是热噪声的另一种表现形式,它困扰着低级模拟甚至数字电子电路,尽管在这种情况下形式不同。
显然,越冷越好。大多数量子系统使用所谓的稀释制冷机来达到低至 10 mK,但一些量子比特的温度可以低至 50 mK,并且很难让这些“落伍者”进一步冷却。因此,某些量子比特不处于逻辑 0 基态,但处于激发状态的可能性很小,但很有可能,因此在后续计算中会出错。
稀释制冷
您可以在我当地的电器商店购买稀释冰箱吗?简短的回答:不。它基于实现极寒的完全不同的原理。系统中没有像消费类或工业冰箱那样的压缩机或电机,但差异远不止于此。
稀释制冷机混合氦同位素,可以将物体冷却到大约 10 mK,在低温区域没有移动部件。它已经存在了大约 50 年,当然也得到了改进。
这个冰箱背后的概念有点违反直觉,许多与量子相关的函数也是如此。稀释装置的冷却能力来自氦-3 (He-3) 和氦-4 (He-4) 同位素混合物的混合热量。氦气的不寻常特性使这一点成为可能:它的两种同位素可以在最低温度下保持溶解,而其他流体往往在足够低的温度下完全分离。
首先,一些背景:He-3 和 He-4 代表两种不同的基本粒子。He-3 是费米子,而 He-4 是玻色子。玻色子可以经历一种称为玻色-爱因斯坦缩合的现象,其中多个粒子可以占据最低的量子力学能态(与“凝聚”的常规含义完全无关)。这种现象是导致 He-4 在饱和蒸气压下在 2.17 K 处开始超流动的原因。
超流动性是流动时没有摩擦或粘度的特性,因此不会损失任何动能。当搅拌时,超流体会形成继续无限旋转的涡流。它在概念上有点类似于超导,但却是一种非常不同的现象。
对于费米子,玻色子现象是不可能的,因为只允许两个费米子(具有相反的自旋)占据相同的量子力学能态。因此,He-3 中的超流体状态更难实现,并且在稀释冰箱的工作温度范围内不会发生。正常流体 He-3 也称为费米流体。
稀释制冷机利用氦的两种同位素 He-3 和 He-4 的混合热来获得冷却。在低于约 0.87 K 的温度下(确切的温度取决于 He-3 浓度),He-3 加 He-4 混合物将分离成两相:富 He-3 相(浓缩相)和 He-3 贫相(稀相),如图 1 所示。
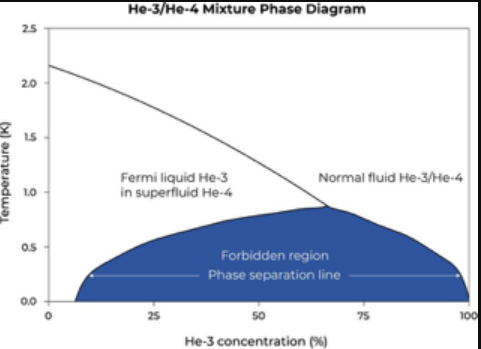
图 1.氦 3 和氦 4 混合物的相图控制稀释制冷过程。(图片来源:Bluefors OY/芬兰)
当温度接近绝对零度时,浓缩相变成纯 He-3,而约 6.6% 的 He-3 保留在稀的富 He-3 相中。He-3 在稀相中的焓大于在浓相中的焓,因此需要能量将 He-3 原子从浓相移动到稀相。
在稀释冰箱中,这种能量取自隔热环境,因此会发生冷却。稀释装置提供的冷却基于 He-3 在泵入稀相时需要热量,从而在发生这种情况的环境中提供冷却。
本文的第 2 部分着眼于稀释冰箱的物理结构。



评论